
【題目】如圖,在△ABC中,AB=AC,點D是BC的中點,點E在AD上.
求證:(1)△ABD≌△ACD;
(2)BE=CE.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知:A=2x2+ax﹣5y+b,B=bx2﹣![]() x﹣
x﹣![]() y﹣3.
y﹣3.
(1)求3A﹣(4A﹣2B)的值;
(2)當x取任意數值,A﹣2B的值是一個定值時,求(a+![]() A)﹣(2b+
A)﹣(2b+![]() B)的值.
B)的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=﹣![]() x+8與x軸、y軸分別相交于點A、B,設M是OB上一點,若將△ABM沿AM折疊,使點B恰好落在x軸上的點B′處.求:
x+8與x軸、y軸分別相交于點A、B,設M是OB上一點,若將△ABM沿AM折疊,使點B恰好落在x軸上的點B′處.求:
(1)點B′的坐標;
(2)直線AM所對應的函數關系式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,轉盤上1、2、3、4四個數字分別代表雞、猴、鼠、羊四種生肖郵票(每種郵票各兩枚,雞年郵票面值“80分”,其它郵票都是面值“1.20元”),轉動轉盤后,指針每落在某個數字所在扇形一次就表示獲得該種郵票一枚. 
(1)任意轉動轉盤一次,獲得猴年郵票的概率是;
(2)任意轉動轉盤兩次,求獲得的兩枚郵票可以郵寄一封需2.4元郵資的信件的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如下圖所示,直線y=-![]() x+3與坐標軸分別交于點A,B,與直線y=x交于點C,線段OA上的點Q以每秒1個單位的速度從點O出發向點A作勻速運動,運動時間為t秒,連結CQ.
x+3與坐標軸分別交于點A,B,與直線y=x交于點C,線段OA上的點Q以每秒1個單位的速度從點O出發向點A作勻速運動,運動時間為t秒,連結CQ.
(1)求出點C的坐標;
(2)若△OQC是等腰直角三角形,則t的值為________;
(3)若CQ平分△OAC的面積,求直線CQ對應的函數表達式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小張在自家土地上平整出了一塊苗圃,并將這塊苗圃分成了四個長方形區域,其尺寸如圖所示(圖中長度單位:米),小張計劃在這四個區域上按圖中所示分別種植草本花卉 1 號、2 號、3 號、4 號.
(1)用式子表示這塊苗圃的總面積;
(2)已知種植草本花卉 1 號、2 號、3 號、4 號的成本分別是每平方米 4 元、6 元、8 元、10 元.
①用式子表示小張在這塊苗圃上種植草本花卉的總成本;
②當 a=9 時,求小張在這塊苗圃上種植草本花卉的總成本.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有5張背面完全相同的卡片,正面分別寫有 ![]() ,(
,( ![]() )0 ,
)0 , ![]() ,π,2﹣2 . 把卡片背面朝上洗勻后,從中隨機抽取1張,其正面的數字是無理數的概率是 .
,π,2﹣2 . 把卡片背面朝上洗勻后,從中隨機抽取1張,其正面的數字是無理數的概率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有4張寫著以下數字的卡片,請按要求抽出卡片,完成下列各題:
![]()
(1)從中取出2張卡片,使這2張卡片上數字之積最大,最大值是________.
(2)從中取出2張卡片,使這2張卡片上數字之差最小,最小值是________.
(3)從中取出4張卡片,將這4個數字進行加、減、乘、除或乘方等混合運算,使結果為24,請寫出一種符合要求的運算式子________.(注:4個數字都必須用到且只能用一次.)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小平所在的學習小組發現,車輛轉彎時,能否順利通過直角彎道的標準是,車輛是否可以行駛到和路的邊界夾角是45°的位置(如圖1中②的位置).例如,圖2是某巷子的俯視圖,巷子路面寬4m,轉彎處為直角,車輛的車身為矩形ABCD,CD與DE、CE的夾角都是45°時,連接EF,交CD于點G,若GF的長度至少能達到車身寬度,即車輛能通過. 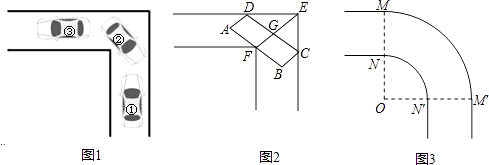
(1)小平認為長8m,寬3m的消防車不能通過該直角轉彎,請你幫他說明理由;
(2)小平提出將拐彎處改為圓弧( ![]() 和
和 ![]() 是以O為圓心,分別以OM和ON為半徑的弧),長8m,寬3m的消防車就可以通過該彎道了,具體的方案如圖3,其中OM⊥OM′,你能幫小平算出,ON至少為多少時,這種消防車可以通過該巷子?
是以O為圓心,分別以OM和ON為半徑的弧),長8m,寬3m的消防車就可以通過該彎道了,具體的方案如圖3,其中OM⊥OM′,你能幫小平算出,ON至少為多少時,這種消防車可以通過該巷子?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com