
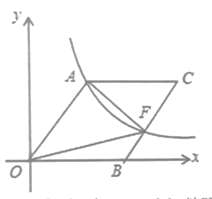
【題目】如圖,在直角坐標系中,四邊形OACB為菱形,OB在x軸的正半軸上,∠AOB=60°,過點A的反比例函數y= ![]() 的圖像與BC交于點F,則△AOF的面積為 ______________.
的圖像與BC交于點F,則△AOF的面積為 ______________.
【答案】4
【解析】
過點A作AM⊥x軸于點M,設OA=a,通過∠AOB的正弦值和余弦值求出AM和OM的長,即可得出點A的坐標,結合反比例函數圖象上點的坐標特征即可求出a的值,再根據四邊形OACB是菱形、點F在邊BC上,即可得出S△AOF=![]() S菱形OBCA,結合菱形的面積公式即可得出結論.
S菱形OBCA,結合菱形的面積公式即可得出結論.
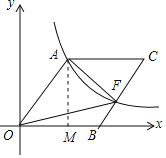
如圖,過點A作AM⊥x軸于點M,設OA=a,
∵∠AOB=60°,
∴AM=a![]() sin60°=
sin60°=![]() a,OM=a
a,OM=a![]() cos60°=
cos60°=![]() a,
a,
∴A點坐標為(![]() a,
a,![]() a),
a),
∵點A在反比例函數y=![]() 圖象上,
圖象上,
∴![]() a
a![]()
![]() a=4,即a2=
a=4,即a2=![]() ,
,
∵四邊形OACB是菱形,點F在邊BC上,
∴S△AOF=![]() S菱形OBCA=
S菱形OBCA=![]() OBAM=
OBAM=![]() ×a
×a![]()
![]() a=
a=![]() a2=
a2=![]() ×
×![]() =4.
=4.
故答案為:4


科目:初中數學 來源: 題型:
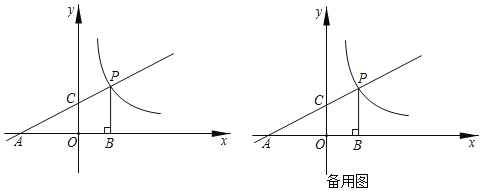
【題目】如圖,已知一次函數![]() 的圖象分別與x軸、y軸交于點A、C,與反比列函數
的圖象分別與x軸、y軸交于點A、C,與反比列函數![]() 的圖象在第一象限內交于點P,過點P作
的圖象在第一象限內交于點P,過點P作![]() 軸,垂足為B,且
軸,垂足為B,且![]() 的面積為9.
的面積為9.
![]() 點A的坐標為______,點C的坐標為______,點P的坐標為______;
點A的坐標為______,點C的坐標為______,點P的坐標為______;
![]() 已知點Q在反比例函數
已知點Q在反比例函數![]() 的圖象上,其橫坐標為6,在x軸上確定一點M,使得
的圖象上,其橫坐標為6,在x軸上確定一點M,使得![]() 的周長最小,求出點M的坐標;
的周長最小,求出點M的坐標;
![]() 設點E是反比例函數
設點E是反比例函數![]() 在第一象限內圖象上的一動點,且點E在直線PB的右側,過點E作
在第一象限內圖象上的一動點,且點E在直線PB的右側,過點E作![]() 軸,垂足為F,當
軸,垂足為F,當![]() 和
和![]() 相似時,求動點E的坐標.
相似時,求動點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+bx+c(a≠0)的對稱軸為直線x=﹣1,圖象經過B(﹣3,0)、C(0,3)兩點,且與x軸交于點A.
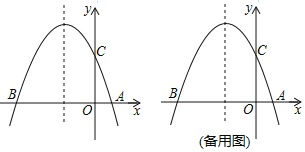
(1)求二次函數y=ax2+bx+c(a≠0)的表達式;
(2)在拋物線的對稱軸上找一點M,使△ACM周長最短,求出點M的坐標;
(3)若點P為拋物線對稱軸上的一個動點,直接寫出使△BPC為直角三角形時點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為改善辦學條件,計劃采購A、B兩種型號的空調,已知采購3臺A型空調和2臺B型空調,需費用39000元;4臺A型空調比5臺B型空調的費用多6000元.
(1)求A型空調和B型空調每臺各需多少元;
(2)若學校計劃采購A、B兩種型號空調共30臺,且A型空調的臺數不少于B型空調的一半,兩種型號空調的采購總費用不超過217000元,該校共有哪幾種采購方案?
(3)在(2)的條件下,采用哪一種采購方案可使總費用最低,最低費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
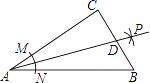
【題目】如圖,在Rt△ABC中,∠C=90°,以A為圓心,以任意長為半徑畫弧,分別交AC、AB于點M、N,再分別以點M、N為圓心,以大于![]() MN的長為半徑畫弧,兩弧相交于點P,作射線AP交BC于點D,若AC=4,BC=3,則CD的長為( )
MN的長為半徑畫弧,兩弧相交于點P,作射線AP交BC于點D,若AC=4,BC=3,則CD的長為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為慶祝國慶節舉辦游園活動,小軍來到摸球兌獎活動場地,李老師對小軍說:“這里有甲、乙兩個盒子,里面都裝有一些乒乓球,你只能選擇在其中一個盒子中摸球。”獲獎規則如下:
甲盒中有白色乒乓球4個,黃色乒乓球1個,一人只能摸一次且一次摸出一個球,若這個球為黃色球,則可獲得玩具熊一個,否則不得獎;
乙盒中有白色乒乓球2個,黃色乒乓球3個,一人只能摸一次且一次摸出兩個球,若這兩個球均為黃色球,則可獲得玩具熊一個,否則不得獎;
請問小軍在哪個盒子內摸球獲得玩具熊的機會更大?請用概率知識說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的一元二次方程x2+3x+m-1=0的兩個實數根分別為x1,x2.
(1)求m的取值范圍.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明從家出發到公園晨練,在公園鍛煉一段時間后按原路返回,同時小明爸爸從公園按小明的路線返回家中,如圖是兩人離家的距離y(米)與小明出發的時間x(分)之間的函數圖象,則下列結論中不正確的是( )
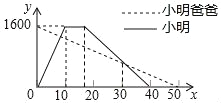
A. 公園離小明家1600米
B. 小明出發![]() 分鐘后與爸爸第一次相遇
分鐘后與爸爸第一次相遇
C. 小明在公園停留的時間為5分鐘
D. 小明與爸爸第二次相遇時,離家的距離是960米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com