
【題目】如圖,在△ABC中,AB=AC=2![]() ,∠BAC=120°,點D、E都在邊BC上,∠DAE=60°.若BD=2CE,則DE的長為_____.
,∠BAC=120°,點D、E都在邊BC上,∠DAE=60°.若BD=2CE,則DE的長為_____.

【答案】3![]() ﹣3.
﹣3.
【解析】
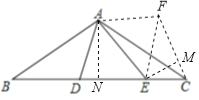
將△ABD繞點A逆時針旋轉120°得到△ACF,連接EF,過點E作EM⊥CF于點M,過點A作AN⊥BC于點N,由AB=AC=2![]() 、∠BAC=120°,可得出BC=6、∠B=∠ACB=30°,通過角的計算可得出∠FAE=60°,結合旋轉的性質可證出△ADE≌△AFE(SAS),進而可得出DE=FE,設CE=2x,則CM=x,EM=
、∠BAC=120°,可得出BC=6、∠B=∠ACB=30°,通過角的計算可得出∠FAE=60°,結合旋轉的性質可證出△ADE≌△AFE(SAS),進而可得出DE=FE,設CE=2x,則CM=x,EM=![]() x、FM=4x-x=3x、EF=ED=6-6x,在Rt△EFM中利用勾股定理可得出關于x的一元二次方程,解之可得出x的值,再將其代入DE=6-6x中即可求出DE的長.
x、FM=4x-x=3x、EF=ED=6-6x,在Rt△EFM中利用勾股定理可得出關于x的一元二次方程,解之可得出x的值,再將其代入DE=6-6x中即可求出DE的長.
將△ABD繞點A逆時針旋轉120°得到△ACF,連接EF,過點E作EM⊥CF于點M,過點A作AN⊥BC于點N,如圖所示,
 ,
,
∵AB=AC=2![]() ,∠BAC=120°,
,∠BAC=120°,
∴BN=CN,∠B=∠ACB=30°,
在Rt△BAN中,∠B=30°,AB=2![]() ,
,
∴AN=![]() AB=
AB=![]() ,BN=
,BN=![]() =3,
=3,
∴BC=6,
∵∠BAC=12°,∠DAE=60°,
∴∠BAD+∠CAE=60°,
∴∠FAE=∠FAC+∠CAE=∠BAD+∠CAE=60°,
在△ADE和△AFE中, ,
,
∴△ADE≌△AFE(SAS),
∴DE=FE,
∵BD=2CE,BD=CF,∠ACF=∠B=30°,
∴設CE=2x,則CM=x,EM=![]() x,FM=4xx=3x,EF=ED=66x.
x,FM=4xx=3x,EF=ED=66x.
在Rt△EFM中,FE=66x,FM=3x,EM=![]() x,
x,
∴EF2=FM2+EM2,,即(66x)2=(3x)2+(![]() x)2,
x)2,
解得:x1=![]() ,x2=
,x2=![]() (不合題意,舍去),
(不合題意,舍去),
∴DE=66x=![]() .
.
故答案為:![]() .
.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:
【題目】在一次綜合實踐活動中,小明要測某地一座古塔AE的高度.如圖,已知塔基頂端B(和A、E共線)與地面C處固定的繩索的長BC為80m.她先測得∠BCA=35°,然后從C點沿AC方向走30m到達D點,又測得塔頂E的仰角為50°,求塔高AE.(人的高度忽略不計,結果用含非特殊角的三角函數表示)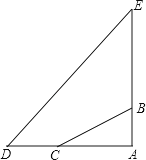
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個小組同時從甲地出發,勻速步行到乙地,甲乙兩地相距7500米,第一組的步行速度是第二組的1.2倍,并且比第二組早15分鐘到達乙地.設第二組的步行速度為x千米/小時,根據題意可列方程是( )
A.![]() ﹣
﹣ ![]() =15
=15
B.![]() ﹣
﹣ ![]() =
= ![]()
C.![]() ﹣
﹣ ![]() =15
=15
D.![]() ﹣
﹣ ![]() =
= ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知|a+b|+|a-b|-2b=0,在數軸上給出關于a,b的四種位置關系如圖所示,則可能成立的有( )
![]()
A. 1種 B. 2種 C. 3種 D. 4種
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:已知正方形的邊長為4,甲、乙兩動點分別從正方形ABCD的頂點A、C同時沿正方形的邊開始移動,甲點依順時針方向環行,乙點依逆時針方向環行,若乙的速度是甲的速度的3倍,則它們第2018次相遇在邊 ( )上.
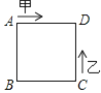
A. AB B. BC C. CD D. DA
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com