
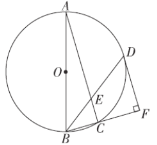
【題目】如圖,AB是⊙O的直徑,△ABC內接于⊙O.點D在⊙O 上,BD平分∠ABC交AC于點E,DF⊥BC交BC的延長線于點F.
(1)求證:FD是⊙O的切線;
(2)若BD=8,sin∠DBF=![]() ,求DE的長.
,求DE的長.
【答案】(1)詳見解析;(2)![]()
【解析】
(1)連接OD,根據角平分線的定義得到∠ABD=∠DBF,由等腰三角形的性質得到∠ABD=∠ODB,等量代換得到∠DBF=∠ODB,推出∠ODF=90°,根據切線的判定定理得到結論;
(2)連接AD,根據圓周角定理得到∠ADE=90°,根據角平分線的定義得到∠DBF=∠ABD,解直角三角形得到AD=6,在Rt△ADE中,解直角三角形得到DE=![]() .
.
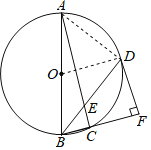
(1)連接OD,
∵BD平分∠ABC交AC于點E,
∴∠ABD=∠DBF,
∵OB=OD,
∴∠ABD=∠ODB,
∴∠DBF=∠ODB,
∵∠DBF+∠BDF=90°,
∴∠ODB+∠BDF=90°,
∴∠ODF=90°,
∴FD是⊙O的切線;
(2)連接AD,
∵AB是⊙O的直徑,
∴∠ADE=90°,
∵BD平分∠ABC交AC于點E,
∴∠DBF=∠ABD,
在Rt△ABD中,BD=8,
∵sin∠ABD=sin∠DBF=![]() ,
,
∴AB=10,AD=6,
∵∠DAC=∠DBC,
∴sin∠DAE=sin∠DBC=![]() ,
,
在Rt△ADE中,sin∠DAC=![]() ,
,
設DE=3x,則AE=5x,
∴AD=4x,
∴tan∠DAE=![]()
∴DE=![]() .
.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于
軸交于![]() 點,經過點
點,經過點![]() 的拋物線
的拋物線![]() 上有一動點
上有一動點![]() ,且點
,且點![]() 在直線
在直線![]() 的下方.
的下方.
(1)平移直線![]() 經過點
經過點![]() ,得到直線
,得到直線![]() ,點
,點![]() 為直線
為直線![]() 上一個動點,連接
上一個動點,連接![]() ,當
,當![]() 面積最大時,求
面積最大時,求![]() 的最小值.
的最小值.
(2)平移直線![]() 經過原點,得到直線
經過原點,得到直線![]() ,點
,點![]() 是直線
是直線![]() 上一點,且
上一點,且![]() 點橫坐標為6,點
點橫坐標為6,點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸上,當
軸上,當![]() 時,拋物線上是否存在點
時,拋物線上是否存在點![]() ,使四邊形
,使四邊形![]() 是矩形?如果存在,請求出點
是矩形?如果存在,請求出點![]() 的坐標,如果不存在,請說明理由.
的坐標,如果不存在,請說明理由.
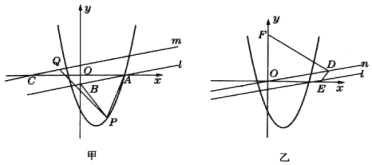
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線EF與⊙O相切于點C,點A為⊙O上異于點C的一動點,⊙O的半徑為4,AB![]() EF于點B,設
EF于點B,設![]() ACF=α(0°<α<180°).
ACF=α(0°<α<180°).
(1)若α=![]() ,求證:四邊形OCBA為正方形;
,求證:四邊形OCBA為正方形;
(2)若AC―AB=1,求AC的長;
(3)當AC―AB取最大值時,求α的度數.
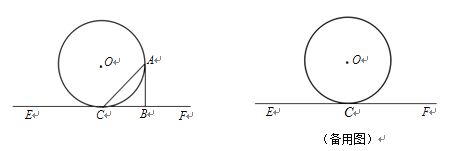
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A在∠MON的邊ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求證:四邊形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表顯示了同學們用計算機模擬隨機投針實驗的某次實驗的結果.
投針次數n | 1000 | 2000 | 3000 | 4000 | 5000 | 10000 | 20000 |
針與直線相交的次數m | 454 | 970 | 1430 | 1912 | 2386 | 4769 | 9548 |
針與直線相交的頻率p=
| 0.454 | 0.485 | 0.4767 | 0.478 | 0.4772 | 0.4769 | 0.4774 |
下面有三個推斷:
①投擲1000次時,針與直線相交的次數是454,針與直線相交的概率是0.454;
②隨著實驗次數的增加,針與直線相交的頻率總在0.477附近,顯示出一定的穩定性,可以估計針與直線相交的概率是0.477;
③若再次用計算機模擬此實驗,則當投擲次數為10000時,針與直線相交的頻率一定是0.4769.
其中合理的推斷的序號是:_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
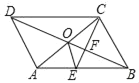
【題目】如圖,ABCD的對角線AC,BD交于點O,CE平分∠BCD交AB于點E,交BD于點F,且∠ABC=60°,AB=2BC,連接OE.下列結論:①∠ACD=30°;②SABCD=ACBC;③OE:AC=![]() :6; ④SOEF=
:6; ④SOEF=![]() SABCD,成立的是_____.
SABCD,成立的是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
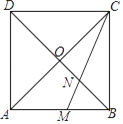
【題目】如圖,正方形ABCD的對角線AC與BD相交于點O,∠ACB的平分線分別交AB、BD于點M、N,若AD=4,則線段AM的長為( )
A. 2B. 2![]() C. 4﹣
C. 4﹣![]() D. 8﹣4
D. 8﹣4![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,點P是BC邊上一動點,連結AP,AP的垂直平分線交BD于點G,交 AP于點E,在P點由B點到C點的運動過程中,∠APG的大小變化情況是( )
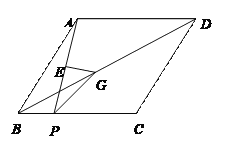
A. 變大 B. 先變大后變小 C. 先變小后變大 D. 不變
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小軍自制的勻速直線運動遙控車模型甲、乙兩車同時分別從![]() 、
、![]() 出發,沿直線軌道同時到達
出發,沿直線軌道同時到達![]() 處,已知乙的速度是甲的速度的1.5倍,甲、乙兩遙控車與
處,已知乙的速度是甲的速度的1.5倍,甲、乙兩遙控車與![]() 處的距離
處的距離![]() 、
、![]() (米)與時間
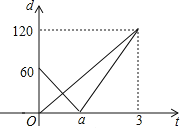
(米)與時間![]() (分鐘)的函數關系如圖所示,則下列結論中:①
(分鐘)的函數關系如圖所示,則下列結論中:①![]() 的距離為120米;②乙的速度為60米/分;③
的距離為120米;②乙的速度為60米/分;③![]() 的值為
的值為![]() ;④若甲、乙兩遙控車的距離不少于10米時,兩車信號不會產生互相干擾,則兩車信號不會產生互相干擾的
;④若甲、乙兩遙控車的距離不少于10米時,兩車信號不會產生互相干擾,則兩車信號不會產生互相干擾的![]() 的取值范圍是
的取值范圍是![]() ,其中正確的有( )個
,其中正確的有( )個
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com