
【題目】如圖,已知拋物線![]() 與坐標軸交于A,B,C三點,其中C(0,3),∠BAC的平分線AE交y軸于點D,交BC于點E,過點D的直線l與射線AC,AB分別交于點M,N.
與坐標軸交于A,B,C三點,其中C(0,3),∠BAC的平分線AE交y軸于點D,交BC于點E,過點D的直線l與射線AC,AB分別交于點M,N.
(1)直接寫出a的值、點A的坐標及拋物線的對稱軸;
(2)點P為拋物線的對稱軸上一動點,若△PAD為等腰三角形,求出點P的坐標;
(3)證明:當直線l繞點D旋轉時,![]() 均為定值,并求出該定值.
均為定值,并求出該定值.

【答案】(1)a=![]() ,A(﹣
,A(﹣![]() ,0),拋物線的對稱軸為x=
,0),拋物線的對稱軸為x=![]() ;(2)點P的坐標為(
;(2)點P的坐標為(![]() ,2)或(
,2)或(![]() ,0)或(
,0)或(![]() ,﹣4);(3)
,﹣4);(3)![]() .
.
【解析】
試題分析:(1)由點C的坐標為(0,3),可知﹣9a=3,故此可求得a的值,然后令y=0得到關于x的方程,解關于x的方程可得到點A和點B的坐標,最后利用拋物線的對稱性可確定出拋物線的對稱軸;
(2)利用特殊銳角三角函數值可求得∠CAO=60°,依據AE為∠BAC的角平分線可求得∠DAO=30°,然后利用特殊銳角三角函數值可求得OD=1,則可得到點D的坐標.設點P的坐標為(![]() ,a).依據兩點的距離公式可求得AD、AP、DP的長,然后分為AD=PA、AD=DP、AP=DP三種情況列方程求解即可;
,a).依據兩點的距離公式可求得AD、AP、DP的長,然后分為AD=PA、AD=DP、AP=DP三種情況列方程求解即可;
(3)設直線MN的解析式為y=kx+1,接下來求得點M和點N的橫坐標,于是可得到AN的長,然后利用特殊銳角三角函數值可求得AM的長,最后將AM和AN的長代入化簡即可.
試題解析:(1)∵C(0,3),∴﹣9a=3,解得:a=![]() .
.
令y=0得:![]() ,∵a≠0,∴
,∵a≠0,∴![]() ,解得:x=﹣
,解得:x=﹣![]() 或x=
或x=![]() ,∴點A的坐標為(﹣
,∴點A的坐標為(﹣![]() ,0),B(
,0),B(![]() ,0),∴拋物線的對稱軸為x=
,0),∴拋物線的對稱軸為x=![]() .
.
(2)∵OA=![]() ,OC=3,∴tan∠CAO=
,OC=3,∴tan∠CAO=![]() ,∴∠CAO=60°.
,∴∠CAO=60°.
∵AE為∠BAC的平分線,∴∠DAO=30°,∴DO=![]() AO=1,∴點D的坐標為(0,1).
AO=1,∴點D的坐標為(0,1).
設點P的坐標為(![]() ,a).
,a).
依據兩點間的距離公式可知:AD2=4,AP2=12+a2,DP2=3+(a﹣1)2.
當AD=PA時,4=12+a2,方程無解.
當AD=DP時,4=3+(a﹣1)2,解得a=2或a=0,∴點P的坐標為(![]() ,2)或(
,2)或(![]() ,0).
,0).
當AP=DP時,12+a2=3+(a﹣1)2,解得a=﹣4,∴點P的坐標為(![]() ,﹣4).
,﹣4).
綜上所述,點P的坐標為(![]() ,2)或(
,2)或(![]() ,0)或(
,0)或(![]() ,﹣4).
,﹣4).
(3)設直線AC的解析式為y=mx+3,將點A的坐標代入得:![]() ,解得:m=
,解得:m=![]() ,∴直線AC的解析式為
,∴直線AC的解析式為![]() .
.
設直線MN的解析式為y=kx+1.
把y=0代入y=kx+1得:kx+1=0,解得:x=![]() ,∴點N的坐標為(
,∴點N的坐標為(![]() ,0),∴AN=
,0),∴AN=![]() =
=![]() .
.
將![]() 與y=kx+1聯立解得:x=
與y=kx+1聯立解得:x=![]() ,∴點M的橫坐標為
,∴點M的橫坐標為![]() .
.
過點M作MG⊥x軸,垂足為G.則AG=![]() .
.
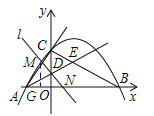
∵∠MAG=60°,∠AGM=90°,∴AM=2AG=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:初中數學 來源: 題型:
【題目】下列說法中正確的是( )
A.兩個全等三角形,一定是軸對稱的
B.兩個軸對稱的三角形,一定全等
C.三角形的一條中線把三角形分成以中線為軸對稱的兩個圖形
D.三角形的一條高把三角形分成以高線為軸對稱的兩個圖形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列不等式變形中正確的是( )
A.若a<b,則a-b<b-1B.若a>b,則ac2>bc2
C.若a-3>-3,則a>0D.若ab>0,則a<0,b<0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】過點(﹣1,7)的直線l與x軸、y軸分別交于點A、B,且與直線y=﹣ ![]() x平行.
x平行.
(1)求直線l的解析式;
(2)寫出在線段AB上,橫、縱坐標都是整數的點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個多邊形的每一個外角都是30度,則它的邊數和每一個內角的度數是( )
A. 12條,30° B. 12條,150° C. 10條,150° D. 8條,150°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 是上半圓的弦,過點
是上半圓的弦,過點![]() 作
作![]() 的切線
的切線![]() 交
交![]() 的延長線于點
的延長線于點![]() ,過點
,過點![]() 作切線
作切線![]() 的垂線,垂足為
的垂線,垂足為![]() ,且與
,且與![]() 交于點
交于點![]() ,設
,設![]() ,
,![]() 的度數分別是
的度數分別是![]() .
.
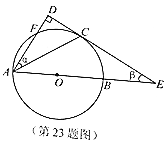
(1)用含![]() 的代數式表示
的代數式表示![]() ,并直接寫出
,并直接寫出![]() 的取值范圍;
的取值范圍;
(2)連接![]() 與
與![]() 交于點
交于點![]() ,當點
,當點![]() 是
是![]() 的中點時,求
的中點時,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,DB∥AC,且DB=![]() AC,E是AC的中點,
AC,E是AC的中點,
(1)求證:BC=DE;
(2)連接AD、BE,若要使四邊形DBEA是矩形,則給△ABC添加什么條件,為什么?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com