【題目】點A（1,n1），點B（2,n2）在一次函數y1=k1x+b1圖像上：點C（3，n3），點D（4，n4）在一次函數y2=k2x+b2圖像上，y1 和y2圖像交點坐標是（m,n）.若n4＜n1＜n3＜n2,則下列說法：①k1＞0，k2＜0；②k1＜0，k2＞0；③1＜m＜3；④2＜m＜4，正確的是____(填序號).
【答案】①③
【解析】
由題可判斷出一次函數y1 和y2的增減性，故可得出①正確，②錯誤；又聯立一次函數表達式，可得出m的代數式變形后由n4＜n1＜n3＜n2，可判斷③正確，④錯誤；
∵點A（1,n1），點B（2,n2）在一次函數y1=k1x+b1圖像上且n1＜n2，
∴y1=k1x+b1隨x增大函數值增大，
∴k1>0，
∵點C（3，n3），點D（4，n4）在一次函數y2=k2x+b2圖像上且n4＜n3，
∴y2=k2x+b2隨x增大函數值減小，
∴k2＜0，
故①正確，②錯誤；
依題意可得一次函數表達式如下，聯立可得
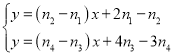
解得
，
∵m=1+
，其中
>0，
m=3+
，其中
<0，
∴1＜m＜3，
故③正確，④錯誤；
故答案為①③.
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】△ABC的三邊分別為
，下列條件能推出△ABC是直角三角形的有（ ）
①
;②
;③ ∠A＝∠B
∠C; ④∠A∶∠B∶∠C＝1∶2∶3 ;⑤
;⑥
A.2個B.3個C.4個D.5個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠B＝∠C，AB＝8，BC＝6，點D為AB的中點，點P在線段BC上以每秒2個單位的速度由點B向點C運動，同時點Q在線段CA上以每秒a個單位的速度由點C向點A運動，設運動時間為t（秒）（0≤t≤3）．
（1）用含t的代數式表示線段PC的長；
（2）若點P、Q的運動速度相等，t＝1時，△BPD與△CQP是否全等，請說明理由．
（3）若點P、Q的運動速度不相等，△BPD與△CQP全等時，求a的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】茂林貨棧打算在年前用 30000 元購進一批彩燈進行銷售，由于進貨廠家促銷，實際可以以 8 折的價格購進這批彩燈，結果可以比計劃多購進了 100 盞彩燈．
⑴該貨棧實際購進每盞彩燈多少元？
⑵該貨棧打算在進價的基礎上，每盞燈加價 30%，進行銷售，該貨棧要想獲得利潤不低于 10000 元，應至少再購進彩燈多少盞？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一個矩形ABCD的較短邊長為2．
（1）如圖①，若沿長邊對折后得到的矩形與原矩形相似，求它的另一邊長；
（2）如圖②，已知矩形ABCD的另一邊長為4，剪去一個矩形ABEF后，余下的矩形EFDC與原矩形相似，求余下矩形EFDC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，
方格紙上的兩條對稱軸
、
相交于中心點
，將格點
（頂點在小正方形的頂點上）分別作下列三種變換：
①先以點
為中心順時針旋轉
，再向右平移
格，最后向上平移格；
②先以點為中心作中心對稱圖形，再以點的對應點為中心逆時針旋轉；
③先以直線為軸作軸對稱圖形，再向上平移格，最后以點的對應點為中心順時針旋轉．
其中，能將變換成
的種數是（ ）
A. 0種 B. 1種 C. 2種 D. 3種
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在等邊三角形ABC，點D在BC上，點E在AG的延長線上，DE＝DA（如圖1）．
（1）求證：∠BAD＝∠EDC；
（2）如圖2，若點E關于直線BC的對稱點為M，連DM，AM，請判斷△ADM的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知
與
是兩個大小不同的等腰直角三角形．
如圖①所示，連接
，
，試判斷線段和的數量和位置關系，并說明理由；
如圖②所示，連接，將線段繞
點順時針旋轉
到
，連接
，試判斷線段
和的數量和位置關系，并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
