
【題目】如圖,BD和CD分別平分△ABC的內角∠EBA和外角∠ECA,BD交AC于F,連接AD. 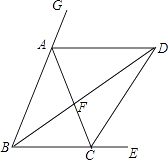
(1)求證:∠BDC= ![]() ∠BAC;
∠BAC;
(2)若AB=AC,請判斷△ABD的形狀,并證明你的結論;
(3)在(2)的條件下,若AF=BF,求∠EBA的大小.
【答案】
(1)解:∵BD、CD分別平分∠EBA、∠ECA,BD交AC于F,
∴∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠ACE,∠BAC+∠ABC=∠ACE,
∠ACE,∠BAC+∠ABC=∠ACE,
∴∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠BAC+
∠BAC+ ![]() ∠ABC,
∠ABC,
∴∠BDC= ![]() ∠BAC
∠BAC
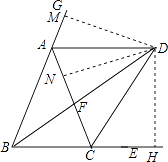
(2)解:△ABD為等腰三角形,證明如下:
作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H
∵BD、CD分別平分∠EBA、∠ECA,
∴DM=DH,DN=DH,
∴DM=DN,
∴AD平分∠CAG,即∠GAD=∠CAD,
∵∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,
∴∠GAD+∠CAD=∠ABC+∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠GAD=∠ABC,
∴AD∥BC,
∴∠ADB=∠DBC,
又∵∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴△ABD為等腰三角形
(3)解:∵AF=BF,
∴∠BAF=∠ABF= ![]() ∠ABC,
∠ABC,
∵∠BAF+∠ABC+∠ACB=180°,∠ABC=∠ACB,
∴ ![]() ∠ABC=180°,
∠ABC=180°,
∴∠ABC=72°.
【解析】(1)根據角平分線的定義得到∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+
∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠BAC+
∠BAC+ ![]() ∠ABC,等量代換即可得到結論;(2)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H根據角平分線的性質得到DM=DH,DN=DH,等量代換得到DM=DN,根據三角形的內角和得到∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,推出∠GAD+∠CAD=∠ABC+∠ACB,由等腰三角形的性質得到∠ABC=∠ACB,等量代換得到∠GAD=∠ABC,推出AD∥BC,由平行線的性質得到∠ADB=∠DBC,證得∠ABD=∠ADB,即可得到結論;(3)根據等腰三角形的性質得到∠BAF=∠ABF=
∠ABC,等量代換即可得到結論;(2)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H根據角平分線的性質得到DM=DH,DN=DH,等量代換得到DM=DN,根據三角形的內角和得到∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,推出∠GAD+∠CAD=∠ABC+∠ACB,由等腰三角形的性質得到∠ABC=∠ACB,等量代換得到∠GAD=∠ABC,推出AD∥BC,由平行線的性質得到∠ADB=∠DBC,證得∠ABD=∠ADB,即可得到結論;(3)根據等腰三角形的性質得到∠BAF=∠ABF= ![]() ∠ABC,根據三角形的內角和即可得到結論.
∠ABC,根據三角形的內角和即可得到結論.


科目:初中數學 來源: 題型:
【題目】判定兩角相等,不對的是( )
A.對頂角相等
B.兩直線平行,同位角相等
C.∵∠1=∠2,∠2=∠3,∴∠1=∠3
D.兩條直線被第三條直線所截,內錯角相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】楊陽同學沿一段筆直的人行道行走,在由A步行到達B處的過程中,通過隔離帶的空隙O,剛好瀏覽完對面人行道宣傳墻上的社會主義核心價值觀標語,其具體信息匯集如下: 如圖,AB∥OH∥CD,相鄰兩平行線間的距離相等,AC,BD相交于O,OD⊥CD.垂足為D,已知AB=20米,請根據上述信息求標語CD的長度.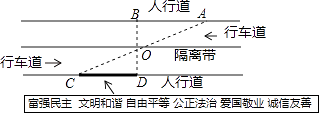
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校有25名同學參加某項比賽,預賽成績各不相同,取前13名參加決賽,其中一名同學已經知道自己的成績,能否進入決賽,只需要再知道這25名同學成績的()
A. 最高分 B. 中位數 C. 方差 D. 平均數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 一次函數是正比例函數
B. 正比例函數是一次函數
C. 不是正比例函數就一定不是一次函數
D. 正比例函數不一定是一次函數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩位同學在一次用頻率估計概率的實驗中統計了某一結果出現的頻率給出的統計圖如圖所示,則符合這一結果的實驗可能是( )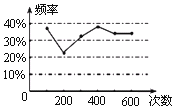
A.擲一枚正六面體的骰子,出現5點的概率
B.擲一枚硬幣,出現正面朝上的概率
C.任意寫出一個整數,能被2整除的概率
D.一個袋子中裝著只有顏色不同,其他都相同的兩個紅球和一個黃球,從中任意取出一個是黃球的概率
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com