
 軸、
軸、 軸建立平面直角坐標系(O、C、F三點在x軸正半軸上).若⊙P過A、B、E三點(圓心在
軸建立平面直角坐標系(O、C、F三點在x軸正半軸上).若⊙P過A、B、E三點(圓心在 軸上),拋物線
軸上),拋物線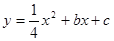 經過A、C兩點,與
經過A、C兩點,與 軸的另一交點為G,M是FG的中點,正方形CDEF的面積為1.
軸的另一交點為G,M是FG的中點,正方形CDEF的面積為1. ,△ACQ的面積 S△ACQ=
,△ACQ的面積 S△ACQ= ,直接寫出
,直接寫出 與
與 之間的函數關系式.
之間的函數關系式.
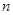
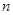 ………1分
………1分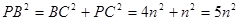
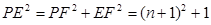
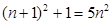
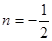 舍去) …………… 2分
舍去) …………… 2分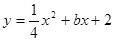 ∴
∴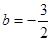
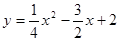 ?
?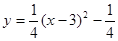 …………………………………………………………… 4分
…………………………………………………………… 4分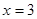 ,即EF所在直線
,即EF所在直線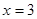 對稱, ∴CF=FG=1 ∴FM=
對稱, ∴CF=FG=1 ∴FM=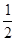 FG=
FG=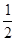
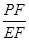 =
=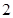 ,
, ∴
∴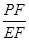 =
=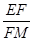 ∴△PEF∽△EMF …………5分
∴△PEF∽△EMF …………5分 ,連
,連 交對稱軸x=3于Q,連AQ
交對稱軸x=3于Q,連AQ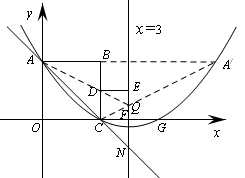
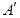 Q,△ACQ周長的最小值為(AC+
Q,△ACQ周長的最小值為(AC+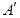 C)的長……………………………7分
C)的長……………………………7分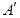 關于直線x=3對稱∴A(0,2),
關于直線x=3對稱∴A(0,2),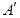 (6,2)
(6,2)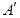 C=
C=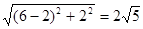 ,
,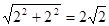 …………………8分
…………………8分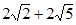 ……………………………9分
……………………………9分

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 )
)查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com