
【題目】某公司有A、B兩種客車,它們的載客量和租金如下表,星星中學根據實際情況,計劃用A、B型車共5輛,同時送七年級師生到校基地參加社會實踐活動.
A | B | |
載客量(人/輛) | 40 | 20 |
租金(元/輛) | 200 | 150 |
(1)若要保證租金費用不超過980元,請問該學校有哪幾種租車方案?
(2)在(1)的條件下,若七年級師生共有150人,問哪種租車方案最省錢?
【答案】
(1)解:設租A型車x輛,則租B型車(5﹣x)輛,
根據題意得:200x+150(5﹣x)≤980,
解得:x≤ ![]() ,
,
∵x取正整數,
∴x=1、2、3、4,
∴該學校的租車方案有:租A型車1輛、B型車4輛;租A型車2輛、B型車3輛;租A型車3輛、B型車2輛;租A型車4輛、B型車1輛
(2)解:設租A型車x輛,則租B型車(5﹣x)輛,
根據題意得:40x+20(5﹣x)≥150,
解得:x≥ ![]() ,
,
∵x取正整數,且x≤ ![]() ,
,
∴x=3或4.
當x=3時,租車費用為200×3+150×2=900(元);
當x=4時,租車費用為200×4+150×1=950(元).
∵900<950,
∴當租A型車3輛、B型車2輛時,租車費用最低
【解析】(1)設租A型車x輛,則租B型車(5﹣x)輛,根據總費用=單價×數量結合租金費用不超過980元,即可得出關于x的一元一次不等式,解之即可得出x的取值范圍,結合x取正整數即可找出各租車方案;(2)設租A型車x輛,則租B型車(5﹣x)輛,根據總人數=單量車的載客量×租車數量結合七年級師生共有150人,即可得出關于x的一元一次不等式,解之即可得出x的取值范圍,結合(1)結論即可確定x的值,再根據總費用=單價×數量求出兩種方案的總費用,比較后即可得出結論.


 每課必練系列答案
每課必練系列答案 巧學巧練系列答案
巧學巧練系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,在Rt△ABC中,∠ACB=90°,∠A=30°,DE垂直平分AC,D為垂足,交AB于E,連接CE. 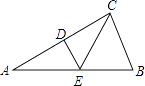
(1)求∠ECB的度數;
(2)若AB=10,求△BCE的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,將△ABC繞點A順時針旋轉90°后得到的△AB′C′(點B的對應點是點B′,點C的對應點是點C′),連接CC′.若∠CC′B′=32°,則∠B的大小是( )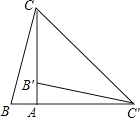
A.32°
B.64°
C.77°
D.87°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】五月初,我市多地遭遇了持續強降雨的惡劣天氣,造成部分地區出現嚴重洪澇災害,某愛心組織緊急籌集了部分資金,計劃購買甲、乙兩種救災物品共2000件送往災區,已知每件甲種物品的價格比每件乙種物品的價格貴10元,用350元購買甲種物品的件數恰好與用300元購買乙種物品的件數相同
(1)求甲、乙兩種救災物品每件的價格各是多少元?
(2)經調查,災區對乙種物品件數的需求量是甲種物品件數的3倍,若該愛心組織按照此需求的比例購買這2000件物品,需籌集資金多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com