
【題目】如圖,四邊形ABCD內接于⊙O,AB是⊙O的直徑,點P在CA的延長線上,∠CAD=45°.
(Ⅰ)若AB=4,求 ![]() 的長;
的長;
(Ⅱ)若 ![]() =
= ![]() ,AD=AP,求證:PD是⊙O的切線.
,AD=AP,求證:PD是⊙O的切線.
【答案】解:(Ⅰ)連接OC,OD, 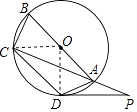
∵∠COD=2∠CAD,∠CAD=45°,
∴∠COD=90°,
∵AB=4,
∴OC= ![]() AB=2,
AB=2,
∴ ![]() 的長=
的長= ![]() ×π×2=π;
×π×2=π;
(Ⅱ)∵ ![]() =
= ![]() ,
,
∴∠BOC=∠AOD,
∵∠COD=90°,
∴∠AOD=45°,
∵OA=OD,
∴∠ODA=∠OAD,
∵∠AOD+∠ODA=∠OAD=180°,
∴∠ODA=67.5°,
∵AD=AP,
∴∠ADP=∠APD,
∵∠CAD=∠ADP+∠APD,∠CAD=45°,
∴∠ADP= ![]() CAD=22.5°,
CAD=22.5°,
∴∠ODP=∠ODA+∠ADP=90°,
∴PD是⊙O的切線.
【解析】(Ⅰ)連接OC,OD,由圓周角定理得到∠COD=2∠CAD,∠CAD=45°,于是得到∠COD=90°,根據弧長公式即可得到結論;(Ⅱ)由已知條件得到∠BOC=∠AOD,由圓周角定理得到∠AOD=45°,根據等腰三角形的性質得到∠ODA=∠OAD,求得∠ADP= ![]() CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到結論.
CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到結論.
【考點精析】根據題目的已知條件,利用圓內接四邊形的性質和切線的判定定理的相關知識可以得到問題的答案,需要掌握把圓分成n(n≥3):1、依次連結各分點所得的多邊形是這個圓的內接正n邊形2、經過各分點作圓的切線,以相鄰切線的交點為頂點的多邊形是這個圓的外切正n邊形;切線的判定方法:經過半徑外端并且垂直于這條半徑的直線是圓的切線.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,BD是△ABC的角平分線,點E,F分別在BC、AB上,且DE∥AB,EF∥AC. 
(1)求證:BE=AF;
(2)若∠ABC=60°,BD=6,求四邊形ADEF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,點D與點B在AC同側,∠DAC>∠BAC,且DA=DC,過點B作BE∥DA交DC于點E,M為AB的中點,連接MD,ME.
(1)如圖1,當∠ADC=90°時,線段MD與ME的數量關系是;
(2)如圖2,當∠ADC=60°時,試探究線段MD與ME的數量關系,并證明你的結論;
(3)如圖3,當∠ADC=α時,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=﹣2,與x軸的一個交點在(﹣3,0)和(﹣4,0)之間,其部分圖象如圖所示,則下列結論:①4a﹣b=0;②c<0;③﹣3a+c>0;④4a﹣2b>at2+bt(t為實數);⑤點(﹣ ![]() ,y1),(﹣
,y1),(﹣ ![]() ,y2),(﹣
,y2),(﹣ ![]() ,y3)是該拋物線上的點,則y1<y2<y3 , 正確的個數有( )
,y3)是該拋物線上的點,則y1<y2<y3 , 正確的個數有( ) 
A.4個
B.3個
C.2個
D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分別是BG,AC的中點. 
(1)求證:DE=DF,DE⊥DF;
(2)連接EF,若AC=10,求EF的長. 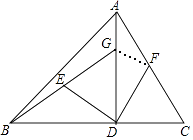
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小瑩和小博士下棋,小瑩執圓子,小博士執方子.如圖,棋盤中心方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示.小瑩將第4枚圓子放入棋盤后,所有棋子構成一個軸對稱圖形.他放的位置是( )
A.(﹣2,1)
B.(﹣1,1)
C.(1,﹣2)
D.(﹣1,﹣2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】本校為了解九年級男同學的體育考試準備情況,隨機抽取部分男同學進行了1000米跑步測試.按照成績分為優秀、良好、合格與不合格四個等級,學校繪制了如下不完整的統計圖. 
(1)根據給出的信息,補全兩幅統計圖;
(2)該校九年級有600名男生,請估計成績未達到良好有多少名?
(3)某班甲、乙兩位成績優秀的同學被選中參加即將舉行的學校運動會1000米比賽.預賽分別為A、B、C三組進行,選手由抽簽確定分組.甲、乙兩人恰好分在同一組的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,E是BC中點,AD是∠BAC的平分線,EF//AD交AC于F.若AB=11,AC=15,則FC的長為( )
A.11
B.12
C.13
D.14
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知命題p,x∈R都有2x<3x , 命題q:x0∈R,使得 ![]() ,則下列復合命題正確的是( )
,則下列復合命題正確的是( )
A.p∧q
B.¬p∧q
C.p∧¬q
D.(¬p)∧(¬q)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com