
 ≥0,∴a-
≥0,∴a- +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 ,只有點a=b時,等號成立.
,只有點a=b時,等號成立. (a,b均為正實數)中,若ab為定值p,則a+b≥
(a,b均為正實數)中,若ab為定值p,則a+b≥ ,只有當a=b時,a+b有最小值2
,只有當a=b時,a+b有最小值2 .
. 有最小值______;
有最小值______; ,并指出等號成立時的條件;
,并指出等號成立時的條件; 上的任意一點,過點P作PC⊥x軸于點C,PO⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
上的任意一點,過點P作PC⊥x軸于點C,PO⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.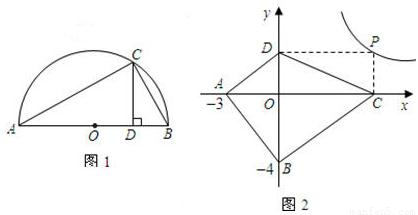
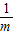 不扣分),最小值為2;
不扣分),最小值為2;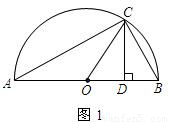
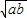 ,
, ,
,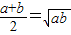 ,
,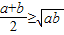 ,即a+b≥2
,即a+b≥2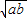 ,當CD等于半徑時,等號成立;
,當CD等于半徑時,等號成立;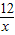 ),
),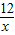 ),CA=x+3,DB=
),CA=x+3,DB=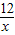 +4,
+4, CA×DB=
CA×DB= (x+3)×(
(x+3)×(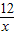 +4),
+4),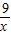 )+12,
)+12,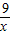 >0,
>0,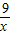 ≥2
≥2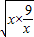 =6,
=6,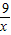 ,即x=3時,等號成立.
,即x=3時,等號成立.

科目:初中數學 來源:2010年浙江省杭州市蕭山區中考數學模擬試卷45(南陽初中 劉東旭 金凱)(解析版) 題型:解答題
 ≥0,∴a-
≥0,∴a- +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 ,只有點a=b時,等號成立.
,只有點a=b時,等號成立. (a,b均為正實數)中,若ab為定值p,則a+b≥
(a,b均為正實數)中,若ab為定值p,則a+b≥ ,只有當a=b時,a+b有最小值2
,只有當a=b時,a+b有最小值2 .
.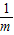 有最小值______;
有最小值______; ,并指出等號成立時的條件;
,并指出等號成立時的條件; 上的任意一點,過點P作PC⊥x軸于點C,PO⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
上的任意一點,過點P作PC⊥x軸于點C,PO⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
查看答案和解析>>
科目:初中數學 來源:2008年全國中考數學試題匯編《反比例函數》(05)(解析版) 題型:解答題
 ≥0,∴a-
≥0,∴a- +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 ,只有點a=b時,等號成立.
,只有點a=b時,等號成立. (a,b均為正實數)中,若ab為定值p,則a+b≥
(a,b均為正實數)中,若ab為定值p,則a+b≥ ,只有當a=b時,a+b有最小值2
,只有當a=b時,a+b有最小值2 .
. 有最小值______;
有最小值______; ,并指出等號成立時的條件;
,并指出等號成立時的條件; 上的任意一點,過點P作PC⊥x軸于點C,PO⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
上的任意一點,過點P作PC⊥x軸于點C,PO⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
查看答案和解析>>
科目:初中數學 來源:2009年浙江省紹興市紹興縣王壇鎮中數學中考模擬試卷(解析版) 題型:解答題
 ≥0,∴a-
≥0,∴a- +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 ,只有點a=b時,等號成立.
,只有點a=b時,等號成立. (a,b均為正實數)中,若ab為定值p,則a+b≥
(a,b均為正實數)中,若ab為定值p,則a+b≥ ,只有當a=b時,a+b有最小值2
,只有當a=b時,a+b有最小值2 .
.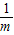 有最小值______;
有最小值______; ,并指出等號成立時的條件;
,并指出等號成立時的條件; 上的任意一點,過點P作PC⊥x軸于點C,PO⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
上的任意一點,過點P作PC⊥x軸于點C,PO⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
查看答案和解析>>
科目:初中數學 來源:2008年江蘇省鹽城市中考數學試卷(解析版) 題型:解答題
 ≥0,∴a-
≥0,∴a- +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 ,只有點a=b時,等號成立.
,只有點a=b時,等號成立. (a,b均為正實數)中,若ab為定值p,則a+b≥
(a,b均為正實數)中,若ab為定值p,則a+b≥ ,只有當a=b時,a+b有最小值2
,只有當a=b時,a+b有最小值2 .
. 有最小值______;
有最小值______; ,并指出等號成立時的條件;
,并指出等號成立時的條件; 上的任意一點,過點P作PC⊥x軸于點C,PO⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
上的任意一點,過點P作PC⊥x軸于點C,PO⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com