
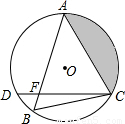
如圖所示,在⊙O中,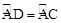 ,弦AB與弦AC交于點A,弦CD與AB交于點F,連接BC.
,弦AB與弦AC交于點A,弦CD與AB交于點F,連接BC.
(1)求證:AC2=AB•AF;
(2)若⊙O的半徑長為2cm,∠B=60°,求圖中陰影部分面積.
(1)證明見解析(2)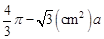
【解析】(1)證明:∵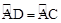 ,∴∠ACD=∠ABC。
,∴∠ACD=∠ABC。
又∵∠BAC=∠CAF,∴△ACF∽△ABC。
∴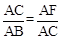 ,即AC2=AB•AF。
,即AC2=AB•AF。
(2)解:如圖,連接OA,OC,過O作OE⊥AC,垂足為點E,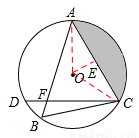
∵∠ABC=60°,∴∠AOC=120°。
又∵OA=OC,∴∠AOE=∠COE= ×120°=60°。
×120°=60°。
在Rt△AOE中,OA=2, OE=OAcos60°=1
∴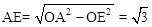 。∴AC=2AE=2
。∴AC=2AE=2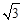 。
。
∴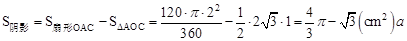 。
。
(1)由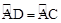 ,利用等弧所對的圓周角相等得到一對角相等,再由一對公共角相等,利用兩對對應角相等的兩三角形相似可得出△ACF∽△ABC,根據相似得比例可得證。
,利用等弧所對的圓周角相等得到一對角相等,再由一對公共角相等,利用兩對對應角相等的兩三角形相似可得出△ACF∽△ABC,根據相似得比例可得證。
(2)連接OA,OC,過O作OE垂直于AC,垂足為點E,由扇形AOC的面積﹣△AOC的面積表示出陰影部分的面積,利用等腰三角形的性質,勾股定理,銳角三角函數定義求出各線段長即可


科目:初中數學 來源: 題型:
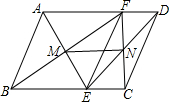 如圖所示,在?ABCD中,EF∥AB且交BC于點E,交AD于點F,連接AE,BF交于點M,連接CF,DE交于點N,求證:MN∥AD且MN=
如圖所示,在?ABCD中,EF∥AB且交BC于點E,交AD于點F,連接AE,BF交于點M,連接CF,DE交于點N,求證:MN∥AD且MN=| 1 | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com