
【題目】如圖,AB是⊙O的直徑,∠BAC=90°,四邊形EBOC是平行四邊形,EB交⊙O于點D,連接CD并延長交AB的延長線于點F.
(1)求證:CF是⊙O的切線;
(2)若∠F=30°,EB=6,求圖中陰影部分的面積(結果保留根號和π)

【答案】(1)證明見解析;(2)9![]() ﹣3π
﹣3π
【解析】試題分析:(1)、連接OD,根據平行四邊形的性質得出∠AOC=∠OBE,∠COD=∠ODB,結合OB=OD得出∠DOC=∠AOC,從而證明出△COD和△COA全等,從而的得出答案;(2)、首先根據題意得出△OBD為等邊三角形,根據等邊三角形的性質得出EC=ED=BO=DB,根據Rt△AOC的勾股定理得出AC的長度,然后根據陰影部分的面積等于兩個△AOC的面積減去扇形OAD的面積得出答案.
試題解析:(1)如圖連接OD.
∵四邊形OBEC是平行四邊形,∴OC∥BE,∴∠AOC=∠OBE,∠COD=∠ODB,
∵OB=OD,∴∠OBD=∠ODB,∴∠DOC=∠AOC,
在△COD和△COA中,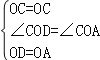 ,∴△COD≌△COA,∴∠CDO=∠CAO=90°,
,∴△COD≌△COA,∴∠CDO=∠CAO=90°,
∴CF⊥OD, ∴CF是⊙O的切線.
(2)∵∠F=30°,∠ODF=90°,∴∠DOF=∠AOC=∠COD=60°,
∵OD=OB,∴△OBD是等邊三角形,∴∠4=60°,∵∠4=∠F+∠1,∴∠1=∠2=30°,
∵EC∥OB,∴∠E=180°﹣∠4=120°,∴∠3=180°﹣∠E﹣∠2=30°,∴EC=ED=BO=DB,
∵EB=6,∴OB=OD═OA=3, 在Rt△AOC中,∵∠OAC=90°,OA=3,∠AOC=60°,
∴AC=OAtan60°=3![]() , ∴S陰=2S△AOC﹣S扇形OAD=2×
, ∴S陰=2S△AOC﹣S扇形OAD=2×![]() ×3×3
×3×3![]() ﹣
﹣![]() =9
=9![]() ﹣3π.
﹣3π.


科目:初中數學 來源: 題型:
【題目】某果園2017年水果產量為100噸,2019年水果產量為196噸,求該果園水果產量的年平均增長率.設該果園水果產量的年平均增長率為x,則根據題意可列方程為( )
A. 196(1﹣x)2B. 100(1﹣x)2=196;C. 196(1+x)2=100;D. 100(1+x)2=196
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把△ABC紙片沿DE折疊,當點A落在四邊形BCDE內部時,則∠A與∠1+∠2之間有一種數量關系始終保持不變,請試著找一找這個規律,這個規律是( )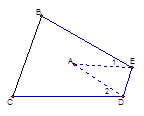
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com