
如圖:在△ABC中,∠C=90°,AD平分∠CAB交BC于點D,AB=10,AC=6,求D到AB的距離.

 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
閱讀理解:
如圖1,在四邊形ABCD的邊AB上任取一點E(點E不與點A、點 B重合),分別連接ED,EC,可以把
B重合),分別連接ED,EC,可以把
四邊形ABCD分成三個三角形,如果其中有兩個三角形相似,我們就把E叫做四邊形ABCD的邊AB上
的相似點;如果這三個三角形都相似,我們就把E叫做四邊形ABCD的邊AB上的強相似點.解決問題:
(1)如圖1,∠A=∠B=∠DEC=55°,試判斷點E是否是四邊形AB CD的邊AB上的相似點,并說明理由;
CD的邊AB上的相似點,并說明理由;
(2)如圖2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四點均在正方形網格(網格中每個小正方
形的邊長為1 )的格點(即每個小正方形的頂點)上,試在圖2中畫出矩形ABCD的邊AB上的一個強相似點E;
)的格點(即每個小正方形的頂點)上,試在圖2中畫出矩形ABCD的邊AB上的一個強相似點E;
拓展探究:
(3)如圖3,將矩形ABCD沿CM折疊,使點D落在AB邊上的點E處.若點E恰好是四邊形ABCM的邊AB上的一個強相似點,試探究AB和BC的數量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
現有三個自愿獻血者,兩人血型為O型,一人血型為A型.若在三人中隨意挑選一人獻血,兩年以后又從此三人中隨意挑選一人獻血,試求兩次所獻血的血型均為O型的概率(要求:用列表或畫樹狀圖的方法解答).
查看答案和解析>>
科目:初中數學 來源: 題型:
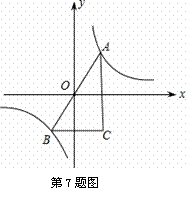
如圖,A,B是反比例函數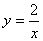 的圖象上關于原點對稱的任意兩點,BC∥x軸,AC∥y軸,△ABC
的圖象上關于原點對稱的任意兩點,BC∥x軸,AC∥y軸,△ABC 的面積記為S,則
的面積記為S,則
A.S = 2 B. 2<S<4 C.S = 4 D.S>4
查看答案和解析>>
科目:初中數學 來源: 題型:
(1)如圖1,在等邊△ABC中,點M是邊BC上的任意一點(不含端點B、C),聯結AM,以AM為邊作等邊△AMN,聯結CN.求證:∠ABC=∠ACN.
【類比探究】
(2)如圖2,在等邊△ABC中,點M是邊BC延長線上的任意一點(不含端點C),其它條件不變,(1)中結論∠ABC=∠ACN還成立嗎?請說明理由.
【拓展延伸】
(3)如圖3,在等腰△ABC中,BA=BC,點M是邊BC上的任意一點(不含端點B、C),聯結AM,以AM為邊作等腰△AMN,使頂角∠AMN=∠ABC.聯結CN.試探究∠ABC與∠ACN的數量關系,并說明理由.
 xkb1.com
xkb1.com
查看答案和解析>>
科目:初中數學 來源: 題型:
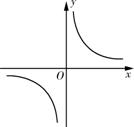
反比例函數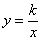 的圖象如圖所示,以下結論:①常數
的圖象如圖所示,以下結論:①常數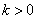 ;②當
;②當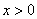 時,函數值
時,函數值 ;③
;③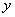 隨
隨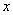 的增大而減小;④若點
的增大而減小;④若點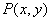 在此函數圖象上,則點
在此函數圖象上,則點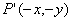 也在此函數圖象上.其中正確的是 ( )
也在此函數圖象上.其中正確的是 ( )
A.①②③④ B.①②③  C.①②④ D.②③④
C.①②④ D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
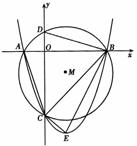
如圖,在平面直角坐標系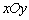 中,以點
中,以點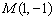 為圓心,以
為圓心,以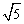 為半徑作圓,與x軸交于A、B兩點,與y軸交于C、D兩點,二次函數
為半徑作圓,與x軸交于A、B兩點,與y軸交于C、D兩點,二次函數 的圖象經
的圖象經
過點A、B、C,頂點為E.
(1)求此二次函數的表達式;
(2)設∠DBC=a,∠CBE=b,求sin(a-b)的值;
(3)坐標軸上是否存在點P,使得以P、A、C為頂點的三角形與△BCE相似.若存在,請直接寫出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
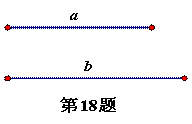
古希臘數學家丟番圖(公元250年前后)在《算術》中就提到了一元二次方程的問題,不過當時古希臘人還沒有尋求到它的求根公式,只能用圖解等方法來求解。在歐幾里得的《幾何原本》中,形如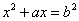 (a>0,b>0)的方程的圖解法是:以
(a>0,b>0)的方程的圖解法是:以 和b為兩直角邊做Rt△ABC,再在斜邊上截取BD=
和b為兩直角邊做Rt△ABC,再在斜邊上截取BD= ,則AD的長就是所求方程的解。
,則AD的長就是所求方程的解。
(1)請利用所給的線段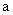 和線段b,作出方程的解。
和線段b,作出方程的解。
(2)說說上述求法的不足之處
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com