
【題目】如圖,平面直角坐標系中,正方形![]() 的頂點
的頂點![]() ,
,![]() ,點
,點![]() 為
為![]() 邊上一動點(不與端點
邊上一動點(不與端點![]() 重合),連接
重合),連接![]() ,作線段
,作線段![]() 的垂直平分線
的垂直平分線![]() 交邊
交邊![]() 于點
于點![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() .
.
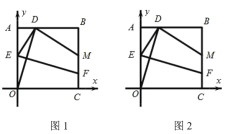
(1)如圖1,當點![]() 為線段AB的中點時,求線段
為線段AB的中點時,求線段![]() 的長;
的長;
(2)如圖2,若正方形![]() 的周長為
的周長為![]() ,
,![]() 的周長為
的周長為![]() ,記
,記![]() ,試證明
,試證明![]() 為定值;
為定值;
(3)在(2)的條件下,構造過點C的拋物線![]() 同時滿足以下兩個條件:
同時滿足以下兩個條件:
①![]() ;②當
;②當![]() 時,函數
時,函數![]() 的最大值為
的最大值為![]() ,求二次項系數
,求二次項系數![]() 的值.
的值.
【答案】(1)![]() ;(2)見解析;(3)二次項系數
;(2)見解析;(3)二次項系數![]() 的值為
的值為![]() 或
或![]() .
.
【解析】
(1)設![]() ,根據勾股定理列方程可得
,根據勾股定理列方程可得![]() 的值,從而得DE,AE的值,證明△AED∽△BDM,利用相似三角形的性質可得DM的長; (2)正方形OABC的周長為
的值,從而得DE,AE的值,證明△AED∽△BDM,利用相似三角形的性質可得DM的長; (2)正方形OABC的周長為![]() ,設
,設![]() ,表示
,表示![]() ,根據勾股定理建立
,根據勾股定理建立![]() 之間的關系式,由(1)中的相似列比例式可表示BM ,DM ,計算△BMD的周長為
之間的關系式,由(1)中的相似列比例式可表示BM ,DM ,計算△BMD的周長為![]() ,代入可求得m的值; (3)先利用
,代入可求得m的值; (3)先利用![]() 與已知條件得到
與已知條件得到![]() 與
與![]() 的關系,寫出拋物線的解析式,可得對稱軸,將(2)中的m代入:得到3≤x≤7時,y有最大值,按開口方向分情況討論可得結論.
的關系,寫出拋物線的解析式,可得對稱軸,將(2)中的m代入:得到3≤x≤7時,y有最大值,按開口方向分情況討論可得結論.
解:(1)設![]() ,依題意有:
,依題意有:![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,解得
,解得![]() .
.
∵ED⊥DM, ∴∠EDM=∠ADE+∠BDM=90°,
∵∠ADE+∠AED=90°, ∴∠AED=∠EDM,
∵∠DAE=∠MBD=90°,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即線段
,即線段![]() 的長為
的長為![]() .
.
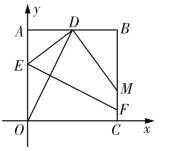
(2)設![]() ,
,![]() ,則有
,則有![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,整理得:
,整理得:![]() .
.
由![]() 可得:
可得:![]() ,
,
從而有:![]() ,可得
,可得![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,將
,將![]() 代入,可得
代入,可得![]() .
.
又∵![]() ,∴
,∴![]() ;∴
;∴![]() 為定值.
為定值.
(3)∵拋物線![]() 經過
經過![]() ,∴
,∴![]() ,
,
由![]() ,可得
,可得![]() ,
,
∴![]()
![]() ,其對稱軸為
,其對稱軸為![]() .
.
由![]() 可知當
可知當![]() 時,函數
時,函數![]() 的最大值為
的最大值為![]() ,
,
于是有:當![]() 時,當
時,當![]() 時有
時有![]() ,此時
,此時![]() ;
;
當![]() 時,當
時,當![]() 時有
時有![]() ,此時
,此時![]() .
.
綜上所述,二次項系數![]() 的值為
的值為![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,直線y=x+3與x軸交于點A,與y軸交于點B,拋物線y=a![]() +bx+c(a<0)經過點A,B,
+bx+c(a<0)經過點A,B,
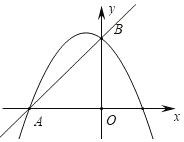
(1)求a、b滿足的關系式及c的值,
(2)當x<0時,若y=a![]() +bx+c(a<0)的函數值隨x的增大而增大,求a的取值范圍,
+bx+c(a<0)的函數值隨x的增大而增大,求a的取值范圍,
(3)如圖,當a=1時,在拋物線上是否存在點P,使△PAB的面積為![]() ?若存在,請求出符合條件的所有點P的坐標;若不存在,請說明理由,
?若存在,請求出符合條件的所有點P的坐標;若不存在,請說明理由,
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣![]() (x+1)(x﹣9)與坐標軸交于A、B、C三點,D為頂點,連結AC,BC.點P是該拋物線在第一象限內上的一點.過點P作y軸的平行線交BC于點E,連結AP交BC于點F,則
(x+1)(x﹣9)與坐標軸交于A、B、C三點,D為頂點,連結AC,BC.點P是該拋物線在第一象限內上的一點.過點P作y軸的平行線交BC于點E,連結AP交BC于點F,則![]() 的最大值為_______.
的最大值為_______.
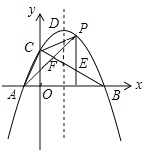
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線![]() 與
與![]() 軸正半軸交于
軸正半軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 左側),與
左側),與![]() 軸交于點
軸交于點![]() .
.
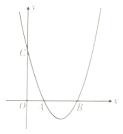
(1)利用直尺和圓規,作出拋物線![]() 的對稱軸(尺規作圖,保留作圖痕跡,不寫作法);
的對稱軸(尺規作圖,保留作圖痕跡,不寫作法);
(2)若![]() 是等腰直角三角形,且其腰長為3,求
是等腰直角三角形,且其腰長為3,求![]() 的值;
的值;
(3)在(2)的條件下,點![]() 為拋物線對稱軸上的一點,則
為拋物線對稱軸上的一點,則![]() 的最小值為________.
的最小值為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某農戶計劃用長12m的籬笆圍成一個“日”字形的生物園飼養兩種不同的家禽,生物園的一面靠墻,且墻的可利用長度最長為7m.
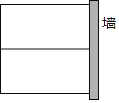
(1)若生物園的面積為9m2,則這個生物園垂直于墻的一邊長為多少?
(2)若要使生物園的面積最大,該怎樣圍?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了豐富同學們的課余生活,某學校舉行“親近大自然”戶外活動,現隨機抽取了部分學生進行主題為“你最想去的景點是?”的問卷調查,要求學生只能從“![]() (植物園)、
(植物園)、![]() (動物園)、
(動物園)、![]() (濕地公園)、
(濕地公園)、![]() (岳麓山)”四個景點中選擇一個,根據調查結果,繪制了兩幅不完整的統計圖.
(岳麓山)”四個景點中選擇一個,根據調查結果,繪制了兩幅不完整的統計圖.
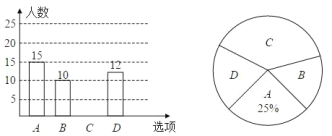
(1)這次問卷調查的人數是_________人;
(2)補全條形統計圖;
(3)計算“![]() ”所在扇形的圓心角度數為_________;
”所在扇形的圓心角度數為_________;
(4)若該學校共有3000名學生,則估計該校最想去岳麓山的學生約為_________人.
查看答案和解析>>
科目:初中數學 來源: 題型:
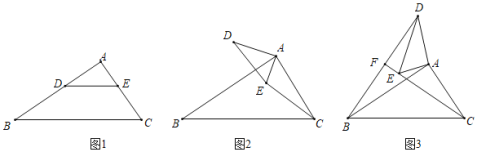
【題目】問題發現:
(1)如圖1,在Rt△ABC中,∠A=90°,AB=kAC(k>1),D是AB上一點,DE∥BC,則BD,EC的數量關系為 .
類比探究
(2)如圖2,將△AED繞著點A順時針旋轉,旋轉角為a(0°<a<90°),連接CE,BD,請問(1)中BD,EC的數量關系還成立嗎?說明理由
拓展延伸:
(3)如圖3,在(2)的條件下,將△AED繞點A繼續旋轉,旋轉角為a(a>90°).直線BD,CE交于F點,若AC=1,AB=![]() ,則當∠ACE=15°時,BFCF的值為_____.
,則當∠ACE=15°時,BFCF的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 的頂點坐標為
的頂點坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,
,![]() 為直線
為直線![]() 下方拋物線上一點,連接
下方拋物線上一點,連接![]() ,
,![]() .
.
(1)求拋物線的解析式.
(2)![]() 的面積是否有最大值?如果有,請求出最大值和此時點
的面積是否有最大值?如果有,請求出最大值和此時點![]() 的坐標;如果沒有,請說明理由.
的坐標;如果沒有,請說明理由.
(3)![]() 為
為![]() 軸右側拋物線上一點,
軸右側拋物線上一點,![]() 為對稱軸上一點,若
為對稱軸上一點,若![]() 是以點
是以點![]() 為直角頂點的等腰直角三角形,請直接寫出點
為直角頂點的等腰直角三角形,請直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com