
【題目】(感知)如圖①在等邊△ABC和等邊△ADE中,連接BD,CE,易證:△ABD≌△ACE;
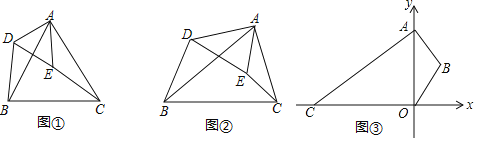
(探究)如圖②△ABC與△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求證:△ABD∽△ACE;
(應用)如圖③,點A的坐標為(0,6),AB=BO,∠ABO=120°,點C在x軸上運動,在坐標平面內作點D,使AD=CD,∠ADC=120°,連結OD,則OD的最小值為 .
【答案】探究:見解析;應用:![]() .
.
【解析】
探究:由△DAE∽△BAC,推出![]() ,可得
,可得![]() ,由此即可解決問題;
,由此即可解決問題;
應用:當點D在AC的下方時,先判定△ABO∽△ADC,得出![]() ,再根據∠BAD=∠OAC,得出△ACO∽△ADB,進而得到∠ABD=∠AOC=90°,得到當OD⊥BE時,OD最小,最后過O作OF⊥BD于F,根據∠OBF=30°,求得OF=
,再根據∠BAD=∠OAC,得出△ACO∽△ADB,進而得到∠ABD=∠AOC=90°,得到當OD⊥BE時,OD最小,最后過O作OF⊥BD于F,根據∠OBF=30°,求得OF=![]() OB=
OB=![]() ,即OD最小值為
,即OD最小值為![]() ;當點D在AC的上方時,作B關于y軸的對稱點B',則同理可得OD最小值為
;當點D在AC的上方時,作B關于y軸的對稱點B',則同理可得OD最小值為![]() .
.
解:探究:如圖②中,
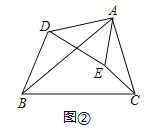
∵∠BAC=∠DAE,∠ABC=∠ADE,
∴△DAE∽△BAC,∠DAB=∠EAC,
∴![]() ,
,
∴![]() ,
,
∴△ABD∽△ACE;
應用:①當點D在AC的下方時,如圖③1中,
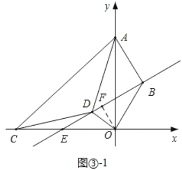
作直線BD,由∠DAC=∠DCA=∠BAO=∠BOA=30°,可得△ABO∽△ADC,
∴![]() ,即
,即![]() ,
,
又∵∠BAD=∠OAC,
∴△ACO∽△ADB,
∴∠ABD=∠AOC=90°,
∵當OD⊥BE時,OD最小,
過O作OF⊥BD于F,則△BOF為直角三角形,
∵A點的坐標是(0,6),AB=BO,∠ABO=120°,
∴易得OB=2![]() ,
,
∵∠ABO=120°,∠ABD=90°,
∴∠OBF=30°,
∴OF=![]() OB=
OB=![]() ,
,
![]() ;
;
當點D在AC的上方時,如圖③2中,
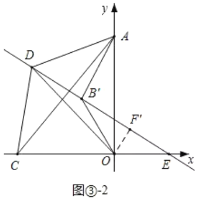
作B關于y軸的對稱點B',作直線DB',則同理可得:△ACO∽△ADB',
∴∠AB'D=∠AOC=90°,
∴當OD⊥B'E時,OD最小,
過O作OF'⊥B'D于F',則△B'OF'為直角三角形,
∵A點的坐標是(0,6),AB'=B'O,∠AB'O=120°,
∴易得OB'=2![]() ,
,
∵∠AB'O=120°,∠AB'D=90°,
∴∠OB'F'=30°,
∴OF'=![]() OB'=
OB'=![]() ,
,
即OD最小值為![]() .
.
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】一條高鐵線A,B,C三個車站的位置如圖所示.已知B,C兩站之間相距530千米.高鐵列車從B站出發,向C站方向勻速行駛,經過13分鐘距A站165千米;經過80分鐘距A站500千米.
![]()
(1)求高鐵列車的速度和AB兩站之間的距離.(2)如果高鐵列車從A站出發,開出多久可以到達C站?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD的邊長為4,P為BC邊上的動點,連接AP,作PQ⊥PA交CD邊于點Q.當點P從B運動到C時,線段AQ的中點M所經過的路徑長( )
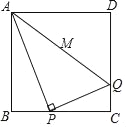
A. 2 B. 1 C. 4 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 是線段
是線段![]() 上任一點,
上任一點,![]() ,
,![]() 兩點分別從
兩點分別從![]() 同時向
同時向![]() 點運動,且
點運動,且![]() 點的運動速度為
點的運動速度為![]() ,
,![]() 點的運動速度為
點的運動速度為![]() ,運動的時間為
,運動的時間為![]() .
.
(1)若![]() ,
,
①運動![]() 后,求
后,求![]() 的長;
的長;
②當![]() 在線段
在線段![]() 上運動時,試說明
上運動時,試說明![]() ;
;
(2)如果![]() 時,
時,![]() ,試探索
,試探索![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法:①![]() 必是負數;②絕對值最小的數是0;③在數軸上,原點兩旁的兩個點表示的數必互為相反數;④在數軸上,左邊的點比右邊的點所表示的數大,其中正確的有( )
必是負數;②絕對值最小的數是0;③在數軸上,原點兩旁的兩個點表示的數必互為相反數;④在數軸上,左邊的點比右邊的點所表示的數大,其中正確的有( )
A.0個B.1個C.2個D.3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,AB=4, ![]() O是以AB為直徑的圓,以B為圓心,1為半徑畫弧與
O是以AB為直徑的圓,以B為圓心,1為半徑畫弧與![]() O交于點C,連接AC.請按下列要求回答問題:
O交于點C,連接AC.請按下列要求回答問題:
①sin![]() A等于____________;
A等于____________;
②在線段AB上取一點E,當BE=______________時,連接CE,使線段CE與圖中弦(不含直徑)所夾角的正弦值等于![]() ;
;
(2)完成操作:僅用無刻度的直尺和圓規作一個直角三角形ABC,使![]() A的正弦值
A的正弦值
等于![]() .(保留作圖痕跡,不必說明作法和理由)
.(保留作圖痕跡,不必說明作法和理由)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店第一次購進相同鉛筆1000支,第二次又購進同種鉛筆,購進數量是第一次的![]() ,這次每支鉛筆的進價比第一次進價高0.2元,第二次購進鉛筆比第一次少花300元.
,這次每支鉛筆的進價比第一次進價高0.2元,第二次購進鉛筆比第一次少花300元.
(1)求第一次每支鉛筆的進價是多少元?
(2)第一次購進鉛筆在第一次進價的基礎上加價50%出售;第二次購進的鉛筆以每支1.5元的價格出售,出售一部分后又在每支1.5元的基礎上打八折出售;兩次購進的鉛筆全部銷售完畢后總獲利為560元,問第二次購進的鉛筆出售多少支后打八折出售?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com