
【題目】閱讀并探究下列問題:

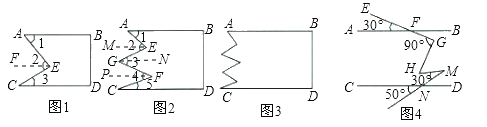
(1)如圖1,將長方形紙片剪兩刀,其中AB∥CD,則∠2與∠1、∠3有何關系?為什么?
(2)如圖2,將長方形紙片剪四刀,其中AB∥CD,則∠2+∠4與∠1+∠3+∠5有何關系?為什么?
(3)如圖3,將長方形紙片剪n刀,其中AB∥CD,你又有何發現?
(4)如圖4,直線AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,則∠GHM= .
【答案】(1)∠2=∠1+∠3;(2)∠2+∠4=∠1+∠3+∠5;(3)開口向左的角的度數的各等于開口向右的角的度數的和;(4)40°.
【解析】
(1)過E點作EF∥AB,則EF∥CD,根據兩直線平行,內錯角相等得到∠AEF=∠1,∠CEF=∠3,即有∠2=∠1+∠3;
(2)分別過E、G、F分別作EM∥AB,GN∥AB,FP∥AB,根據兩直線平行,內錯角相等,同(1)一樣易得到∠2+∠4=∠1+∠3+∠5;
(3)綜合(1)(2)易得開口向左的角的度數的各等于開口向右的角的度數的和.
(4)利用(3)的結論得到∠BFG+∠GHM+∠MND=∠FGH+∠HMN,易計算出∠GHM.
(1)圖1中,∠2=∠1+∠3.理由如下:
過E點作EF∥AB,如圖,
則EF∥CD,
∴∠AEF=∠1,∠CEF=∠3,
∴∠2=∠1+∠3
(2)圖2中,分別過E、G、F分別作EM∥AB,GN∥AB,FP∥AB,
同(1)的證明方法一樣可得∠2+∠4=∠1+∠3+∠5;
(3)圖3中,開口向左的角的度數的各等于開口向右的角的度數的和.
(4)圖4中,由(3)的結論得,∠BFG+∠GHM+∠MND=∠FGH+∠HMN,
∴30°+∠GHM+50°=90°+30°,
∴∠GHM=40°.
故答案為40°.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:
【題目】某次考試中,某班級的數學成績統計圖如圖.下列說法錯誤的是( )

A. 得分在70~80分之間的人數最多 B. 該班的總人數為40
C. 得分在90~100分之間的人數最少 D. 及格(≥60分)人數是26
查看答案和解析>>
科目:初中數學 來源: 題型:
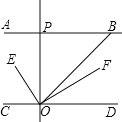
【題目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.則下列結論: ①∠BOE=![]() (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正確結論__________(填編號).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正確結論__________(填編號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊△ABC中,點D為△ABC內的一點,∠ADB=120°,∠ADC=90°,將△ABD繞點A逆時針旋轉60°得△ACE,連接DE.
(1)求證:AD=DE;
(2)求∠DCE的度數;
(3)若BD=1,求AD,CD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】任何一個正整數n都可以進行這樣的分解:n=s×t(s,t是正整數,且s≤t),如果p×q在n的所有這種分解中兩因數之差的絕對值最小,我們就稱p×q是n的最佳分解,并規定:F(n)=![]() .例如18可分解成1×18,2×9,3×6這三種,這時就有F(18)=
.例如18可分解成1×18,2×9,3×6這三種,這時就有F(18)=![]() =
=![]() .給出下列關于F(n)的說法:
.給出下列關于F(n)的說法:
(1)F(2)=![]() ;(2)F(12)=
;(2)F(12)=![]() ;(3)F(27)=3;(4)若n是一個完全平方數,則F(n)=1.
;(3)F(27)=3;(4)若n是一個完全平方數,則F(n)=1.
其中正確說法的個數是( )
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,下列能判定AB∥CD的條件有( )個.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,數軸上A、B兩點分別對應有理數a、b,A、B兩點之間的距離表示為AB,在數軸上A、B兩點之間的距離AB=|a﹣b|,利用數形結合思想回答下列問題:
![]()
(1)數軸上表示2和10兩點之間的距離是 ,數軸上表示2和﹣10兩點之間的距離是 ;
(2)數軸上,x和﹣2兩點之間的距離是 ;
(3)若x表示一個有理數,則|x﹣1|+|x+2|有最小值嗎?若有,請求出最小值,若沒有,寫出理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子里裝有只有顏色不同的黑、白兩種球共40個,小李做摸球實驗,她將盒子里面的球攪勻后從中隨機摸出一個球記下顏色,再把它放回盒子中,不斷重復上述過程,下表是實驗中的一組統計數據:

(1)請估計:當實驗次數為5000次時,摸到白球的頻率將會接近 ;(精確到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)= ;
(3)試驗估算這個不透明的盒子里黑球有多少只?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個汽車零件制造車間可以生產甲,乙兩種零件,生產4個甲種零件和3個乙種零件共獲利120元;生產2個甲種零件和5個乙種零件共獲利130元.
(1)求生產1個甲種零件,1個乙種零件分別獲利多少元?
(2)若該汽車零件制造車間共有工人30名,每名工人每天可生產甲種零件6個或乙種零件5個,每名工人每天只能生產同一種零件,要使該車間每天生產的兩種零件所獲總利潤超過2800元,至少要派多少名工人去生產乙種零件?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com