
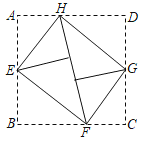
【題目】如圖,將矩形ABCD的四個角向內折起,恰好拼成一個既無縫隙又不重疊的四邊形EFGH,若EH=4,EF=5,那么線段AD與AB的比等于_____.
【答案】![]() .
.
【解析】
先根據圖形翻折的性質可得到四邊形EFGH是矩形,由“AAS”可證Rt△AHE≌Rt△CFG,可得AH=CF=FN,再由勾股定理及直角三角形的面積公式求出AD,AB的長,即可求解.
如圖:
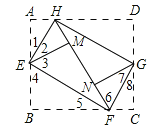
由折疊的性質可得:∠1=∠2,∠3=∠4,AE=EM=BE,DH=HN,CF=FN,
∴∠2+∠3=90°,
∴∠HEF=90°,
同理四邊形EFGH的其它內角都是90°,
∴四邊形EFGH是矩形.
∴EH=FG;
又∵∠1+∠4=90°,∠4+∠5=90°,
∴∠1=∠5,
同理∠5=∠7=∠8,
∴∠1=∠8,
∴Rt△AHE≌Rt△CFG(AAS),
∴AH=CF=FN,
又∵HD=HN,
∴AD=HF,
在Rt△HEF中,EH=4,EF=5,根據勾股定理得HF=![]() =
=![]() =AD,
=AD,
∵S△EFH=![]() ×EF×EH=
×EF×EH=![]() ×HF×EM,
×HF×EM,
∴EM=![]() ,
,
∴AB=2AE=2EM=![]() ,
,
∴AD:AB=41:40=![]() ,
,
故答案為:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線![]() 的圖象經過
的圖象經過![]() 和
和![]() 兩點,且與
兩點,且與![]() 軸交于
軸交于![]() ,直線
,直線![]() 是拋物線的對稱軸,過點
是拋物線的對稱軸,過點![]() 的直線
的直線![]() 與直線相交于點
與直線相交于點![]() ,且點
,且點![]() 在第一象限.
在第一象限.

(1)求該拋物線的解析式;
(2)若直線![]() 和直線
和直線![]() 、
、![]() 軸圍成的三角形面積為6,求此直線的解析式;
軸圍成的三角形面積為6,求此直線的解析式;
(3)點![]() 在拋物線的對稱軸上,
在拋物線的對稱軸上,![]() 與直線
與直線![]() 和
和![]() 軸都相切,求點
軸都相切,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為支持國家南水北調工程建設,小王家由原來養殖戶變為種植戶,經市場調查得知,當種植櫻桃的面積x不超過15畝時,每畝可獲得利潤y=1900元;超過15畝時,每畝獲得利潤y(元)與種植面積x(畝)之間的函數關系如下表(為所學過的一次函數,反比例函數或二次函數中的一種)
x(畝) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)請求出種植櫻桃的面積超過15畝時每畝獲得利潤y與x的函數關系式;
(2)如果小王家計劃承包荒山種植櫻桃,受條件限制種植櫻桃面積x不超過50畝,設小王家種植x畝櫻桃所獲得的總利潤為W元,求小王家承包多少畝荒山獲得的總利潤最大,并求總利潤W(元)的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某無人機興趣小組在操場上開展活動(如圖),此時無人機在離地面30米的D處,無人機測得操控者A的俯角為37°,測得點C處的俯角為45°.又經過人工測量操控者A和教學樓BC距離為57米,求教學樓BC的高度.(注:點A,B,C,D都在同一平面上.參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中數學 來源: 題型:
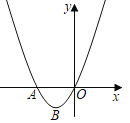
【題目】如圖,拋物線W的圖象與x軸交于A、O兩點,頂點為點B(﹣1,﹣1).
(1)求拋物線W的表達式;
(2)將拋物線W繞點A旋轉180°得到拋物線V,使拋物線V的頂點為E,試通過計算判斷拋物線V是否過點B;
(3)在拋物線W或V的圖象上是否存在點D,使S△EBD=S△EBO?若存在,請求出點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
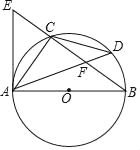
【題目】如圖,⊙O是Rt△ABC的外接圓,∠ACB=90°,點D是![]() 上的一點,且
上的一點,且![]() ,連接AD交BC于點F,過點A作⊙O的切線AE交BC的延長線于點E.
,連接AD交BC于點F,過點A作⊙O的切線AE交BC的延長線于點E.
(1)求證:CF=CE;
(2)若AD=8,AC=5,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某植物園有一塊足夠大的空地,其中有一堵長為a米的墻,現準備用20米的籬笆圍兩間矩形花圃,中間用籬笆隔開.小俊設計了如圖甲和乙的兩種方案:
方案甲中AD的長不超過墻長;方案乙中AD的長大于墻長.
(1)若a=6.
①按圖甲的方案,要圍成面積為25平方米的花圃,則AD的長是多少米?
②按圖乙的方案,能圍成的矩形花圃的最大面積是多少?
(2)若0<a<6.5,哪種方案能圍成面積最大的矩形花圃?請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com