Question

已知關于x的方程（m-1）x²-（2m-1）x+2=0．
（1）求證：無論m取任何實數，方程總有實數根；
（2）若方程只有整數根，求整數m的值．

Answer 1

【答案】分析：（1）利用根的判別式△=b²-4ac直接進行判斷即可；
（2）首先計算出方程的解，再根據方程只有整數根，討論m的值．
解答：（1）證明：∵△=[-（2m-1）]²-4×（m-1）×2=4m²-12m+9=（2m-3）²≥0，
∴無論m取任何實數，方程總有實數根；

（2）x==，
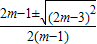
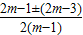
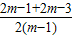
x₁==2，x₂==，
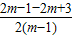
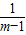
∵方程只有整數根，
∴m-1=±1，
解得：m=0或2．
點評：此題主要考查了根的判別式，關鍵是掌握一元二次方程根的情況與判別式△的關系：
（1）△＞0?方程有兩個不相等的實數根；
（2）△=0?方程有兩個相等的實數根；
（3）△＜0?方程沒有實數根．