
【題目】如圖,矩形ABCD中,以對角線BD為一邊構造一個矩形BDEF,使得另一邊EF過原矩形的頂點C.
(1)設Rt△CBD的面積為S1,Rt△BFC的面積為S2,Rt△DCE的面積為S3,則S1__ __S2+S3;(填“>”“=”或“<”)
(2)寫出圖中的三對相似三角形,并選擇其中一對進行證明.

【答案】△BCD∽△CFB,△BCD∽△DEC,△CFB∽△DEC
【解析】試題分析:(1)根據S1=![]() S矩形BDEF,S2+S3=
S矩形BDEF,S2+S3=![]() S矩形BDEF,即可得出答案.
S矩形BDEF,即可得出答案.
(2)根據矩形的性質,結合圖形可得:△BCD∽△CFB∽△DEC,選擇一對進行證明即可.
試題解析:
(1) ∵S1=![]() BD×ED,S矩形BDEF=BD×ED,
BD×ED,S矩形BDEF=BD×ED,
∴S1=![]() S矩形BDEF,
S矩形BDEF,
∴S2+S3=![]() S矩形BDEF,
S矩形BDEF,
∴S1=S2+S3.
△BCD∽△CFB,△BCD∽△DEC,△CFB∽△DEC.
(2)△BCD∽△CFB∽△DEC.
證明△BCD∽△DEC;
證明:∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°,
∴∠EDC=∠CBD,
又∵∠BCD=∠DEC=90°,
∴△BCD∽△DEC.


科目:初中數學 來源: 題型:
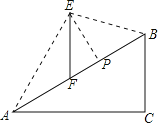
【題目】如圖,在坡度![]() :
:![]() 的斜坡AB上立有一電線桿EF,工程師在點A處測得E的仰角為
的斜坡AB上立有一電線桿EF,工程師在點A處測得E的仰角為![]() ,沿斜坡前進20米到達B,此時測得點E的仰角為
,沿斜坡前進20米到達B,此時測得點E的仰角為![]() ,現要在斜坡AB上找一點P,在P處安裝一根拉繩PE來固定電線桿,以使EF保持豎直,為使拉繩PE最短,則FP的長度約為
,現要在斜坡AB上找一點P,在P處安裝一根拉繩PE來固定電線桿,以使EF保持豎直,為使拉繩PE最短,則FP的長度約為![]() 參考數據:
參考數據:![]()
A. ![]() 米 B.
米 B. ![]() 米 C.
米 C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3cm,動點P從點A出發,沿AB方向以每秒2cm的速度向終點B運動;同時,動點Q從點B出發沿BC力向以每秒1cm的速度向終點C運動,將△PQC翻折,點P的對應點為R,設點Q運動的時間為t秒,若四邊形PCRQ為菱形,則t的值為( )

A. ![]() B. 2C. 1D.
B. 2C. 1D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
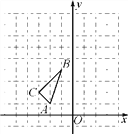
【題目】如圖,在平面直角坐標系中,△ABC的三個頂點坐標分別為A(-2,1),B(-1,4),C(-3,2).
(1)以原點O為位似中心,相似比為1∶2,在y軸的左側,畫出△ABC放大后的圖形△A1B1C1,并直接寫出C1點的坐標;
(2)若點D(a,b)在線段AB上,請直接寫出經過(1)的變化后點D的對應點D1的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
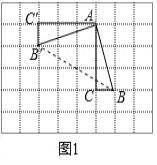
【題目】(1)(操作發現)
如圖 1,在邊長為 1 個單位長度的小正方形組成的網格中,ABC 的三個頂點均在格點上.現將ABC 繞點 A 按順時針方向旋轉 90°,點 B 的對應點為 B′,點 C 的對應點為 C′, 連接 BB′,如圖所示則∠AB′B= .
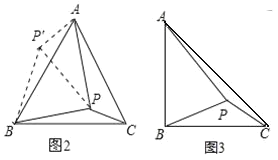
(2)(解決問題)
如圖 2,在等邊ABC 內有一點 P,且 PA=2,PB=![]() ,PC=1,如果將△BPC 繞點 B 順時針旋轉 60°得出△ABP′,求∠BPC 的度數和 PP′的長;
,PC=1,如果將△BPC 繞點 B 順時針旋轉 60°得出△ABP′,求∠BPC 的度數和 PP′的長;
(3)(靈活運用)
如圖 3,將(2)題中“在等邊ABC 內有一點 P 改為“在等腰直角三角形 ABC 內有一點P”,且 BA=BC,PA=6,BP=4,PC=2,求∠BPC 的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)解不等式2(4x-1)≥5x-8,并把它的解集在數軸上表示出來.
![]()
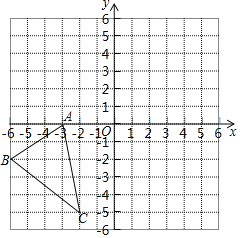
(2)如圖,在平面直角坐標系xOy中,△ABC的三個頂點的坐標分別是A(-3,0),B(-6,-2)C(-2,-5).將△ABC向上平移3個單位長度,再向右平移5個單位長度,得到△A1B1C1.
①在平面直角坐標系xOy中畫出△A1B1C1.
②求△A1B1C1的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
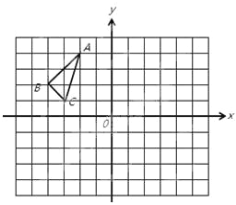
【題目】△ABC 在平面直角坐標系中的位置如圖所示, 其中每個小正方形的邊長為1個單位長度.
(1)△ABC 關于原點 O 的中心對稱圖形為△A1B1C1,寫出點 A 的對應點 A1 的坐標 ;
(2)畫出將△ABC 繞點O 順時針旋轉 90°得到的△A2B2C2;
(3)若 P(a,b)為△ABC 邊上一點,則在△A2B2C2 中,點 P 對應的點 Q 的坐標為 .
(4)請直接寫出:以 A、B、C 為頂點的平行四邊形的第四個頂點 D 的坐標 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】汽車在行駛的過程中速度往往是變化的,如圖表示一輛汽車的速度隨時間變化而變化的情況.
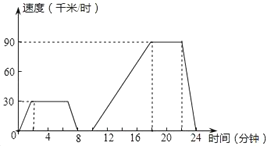
(1)汽車從出發到最后停止共經過了多少時間?它的最高時速是多少?
(2)汽車在哪些時間段保持勻速行駛?時速分別是多少?
(3)汽車出發8min到10min之間可能發生了什么情況?
(4)求汽車從出發后第18分鐘到第22分鐘行駛的路程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校八年級舉行英語演講比賽,準備用1200元錢(全部用完)購買A,B兩種筆記本作為獎品,已知A,B兩種每本分別為12元和20元,設購入A種x本,B種y本.
(1)求y關于x的函數表達式.
(2)若購進A種的數量不少于B種的數量.
①求至少購進A種多少本?
②根據①的購買,發現B種太多,在費用不變的情況下把一部分B種調換成另一種C,調換后C種的數量多于B種的數量,已知C種每本8元,則調換后C種至少有______本(直接寫出答案)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com