
【題目】如圖,線段AB為⊙O的直徑,點C,E在⊙O上,![]() ,CD⊥AB,垂足為點D,連接BE,弦BE與線段CD相交于點F.
,CD⊥AB,垂足為點D,連接BE,弦BE與線段CD相交于點F.
(1)求證:CF=BF;
(2)若cos∠ABE![]() ,在AB的延長線上取一點M,使BM=4,⊙O的半徑為6.求證:直線CM是⊙O的切線.
,在AB的延長線上取一點M,使BM=4,⊙O的半徑為6.求證:直線CM是⊙O的切線.

【答案】(1)證明見解析;(2)證明見解析.
【解析】
(1)延長CD交⊙O于G,如圖,利用垂徑定理得到![]() ,則可證明
,則可證明![]() ,然后根據圓周角定理得∠CBE=∠GCB,從而得到CF=BF ;
,然后根據圓周角定理得∠CBE=∠GCB,從而得到CF=BF ;
(2)連接OC交BE于H,如圖,先利用垂徑定理得到OC⊥BE ,再在Rt△OBH中利用解直角三角形得到BH![]() ,OH
,OH![]() ,接著證明△OHB∽△OCM得到∠OCM=∠OHB=90°,然后根據切線的判定定理得到結論.
,接著證明△OHB∽△OCM得到∠OCM=∠OHB=90°,然后根據切線的判定定理得到結論.
(1)延長CD交⊙O于G,如圖,
∵CD⊥AB,∴![]() ,
,
![]() ,∴
,∴![]() ,
,
∴∠CBE=∠GCB,
∴CF=BF;
(2)連接OC交BE于H,如圖,
∵![]() ,∴OC⊥BE,
,∴OC⊥BE,
在Rt△OBH中,cos∠OBH![]() ,
,
∴BH![]() ,
,
∴OH![]()
![]() ,
,
∴![]() ,而∠HOB=∠COM,
,而∠HOB=∠COM,
∴△OHB∽△OCM,
∴∠OCM=∠OHB=90°,
∴OC⊥CM,
∴直線CM是⊙O的切線.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:初中數學 來源: 題型:
【題目】近幾年杭州市推出了“微公交”,“微公交”是國內首創的純電動汽車租賃服務.它作為一種綠色出行方式,對緩解交通堵塞和停車困難,改善城市大氣環境,都可以起到積極作用.據了解某租賃點擁有“微公交”![]() 輛.據統計,當每輛車的年租金為
輛.據統計,當每輛車的年租金為![]() 千元時可全部租出;每輛車的年租金每增加
千元時可全部租出;每輛車的年租金每增加![]() 千元,未租出的車將增加
千元,未租出的車將增加![]() 輛.
輛.
(1)當每輛車的年租金定為![]() 千元時,能租出多少輛?
千元時,能租出多少輛?
(2)當每輛車的年租金增加多少千元時,租賃公司的年收益(不計車輛維護等其他費用)可達到![]() 千元?
千元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某辦公大樓正前方有一根高度是15米的旗桿ED,從辦公樓頂端A測得旗桿頂端E的俯角α是45°,旗桿底端D到大樓前梯坎底邊的距離DC是20米,梯坎坡長BC是12米,梯坎坡度i=1:![]() ,則大樓AB的高度約為( )(精確到0.1米,參考數據:
,則大樓AB的高度約為( )(精確到0.1米,參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)

A. 30.6 B. 32.1 C. 37.9 D. 39.4
查看答案和解析>>
科目:初中數學 來源: 題型:
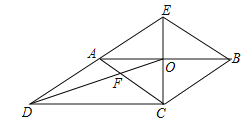
【題目】如圖,CE是ABCD的邊AB的垂直平分線,垂足為點O,CE與DA的延長線交于點E.連接AC,BE,DO,DO與AC交于點F,則下列結論:
①四邊形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S四邊形AFOE:S△COD=2:3.
其中正確的結論有_____.(填寫所有正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖為一座拋物線型的拱橋,AB、CD分別表示兩個不同位置的水面寬度,O為拱橋頂部,水面AB寬為10米,AB距橋頂O的高度為12.5米,水面上升2.5米到達警戒水位CD位置時,水面寬為( )米.

A. 5 B. 2![]() C. 4
C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在2014年巴西世界杯足球賽前夕,某體育用品店購進一批單價為40元的球服,如果按單價60元銷售,那么一個月內可售出240套,根據銷售經驗,提高銷售單價會導致銷售量的減少,即銷售單價每提高5元,銷售量相應減少20套,設銷售單價為x(120>x≥60)元,銷售量為y套.
(1)求出y與x的函數關系式;
(2)當銷售單價為多少元時,月銷售額為14000元,此月共盈利多少元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知網格上最小的正方形的邊長為1.
(1)分別寫出A,B,C三點的坐標;
A_____________;B_____________;C _____________.
(2)作△ABC關于y軸的對稱圖形△A′B′C′;
(3)求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
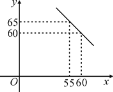
【題目】某體育用品商店試銷一款成本為50元的排球,規定試銷期間單價不低于成本價,且獲利不得高于40%.經試銷發現,銷售量y(個)與銷售單價x(元)之間滿足如圖所示的一次函數關系.
(1)試確定y與x之間的函數關系式;
(2)若該體育用品商店試銷的這款排球所獲得的利潤Q元,試寫出利潤Q(元)與銷售單價x(元)之間的函數關系式;當試銷單價定為多少元時,該商店可獲最大利潤?最大利潤是多少元?
(3)若該商店試銷這款排球所獲得的利潤不低于600元,請確定銷售單價x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com