
【題目】已知:如圖,在矩形ABCD中,AC是對角線.點P為矩形外一點且滿足AP=PC,AP⊥PC.PC交AD于點N,連接DP,過點P作PM⊥PD交AD于M.
(1)若AP=![]() ,AB=
,AB=![]() BC,求矩形ABCD的面積;
BC,求矩形ABCD的面積;
(2)若CD=PM,求證:AC=AP+PN.
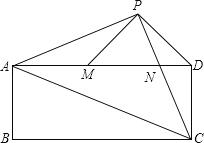
【答案】(1)3(2)AC=AP+PN
【解析】(1)∵AP⊥CP且AP=CP
∴△APC為等腰直角三角形
∵AP=![]()
∴AC=![]() .................1分
.................1分
∵AB=![]() BC
BC
∴設AB=x,BC=3x
∴在Rt△ABC中
x2+(3x)2=10
10x2=10
x=1.................3分
∴![]() .................4分
.................4分
(2)延長AP,CD交于Q
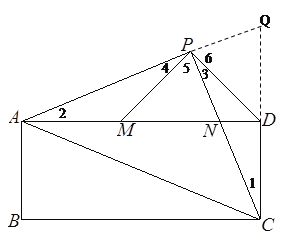
∵∠1+∠CND=∠2+∠PNA=900
且∠CND=∠ANP
∴∠1=∠2
又∠3+∠5=∠4+∠5=900
∴∠3=∠4
又∵AP=CP
∴△APM≌△CPD
∴DP=PM
又∵CD=PM
∴CD=PD
∴∠1=∠3
∠1+∠Q=∠3+∠6=90°
∵∠1=∠3
∴∠Q=∠6
∴DQ=DP=CD
∴D為CQ中點
又∵AD⊥CQ
∴AC=AQ=AP+PQ
又∵∠1=∠2
∠APN=∠CPQ=900
AP=CP ∴△APN≌△CPQ
∴PQ=PN
∴AC=AP+PQ=AP+PN.................10分
(1)由已知條件知△APC為等腰直角三角形,即可求得AC的長,再利用勾股定理求得AB,BC的長,從而求得矩形ABCD的面積
(2)延長AP,CD交于Q,通過角之間的等量關系,求得△APN≌△CPQ,得出PQ=PN,從而求得結論


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F為垂足,則下列四個結論:①∠DEF=∠DFE;②AE=AF;③DA平分∠EDF;④EF垂直平分AD.其中正確的序號是____________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個口袋中有紅球、白球共10個,這些球除顏色外都相同.將口袋中的球攪拌均勻,從中隨機摸出一個球,記下它的顏色后再放回口袋中,不斷重復這一過程,共摸了100次球,發現有70次摸到紅球.請你估計這個口袋中有_____個白球.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,E是AD上一點,PQ垂直平分BE,分別交AD、BE、BC于點P、O、Q,連接BP、EQ.
(1)求證:四邊形BPEQ是菱形;
(2)若AB=6,F為AB的中點,OF+OB=9,求PQ的長.
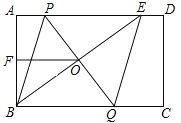
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象過點
的圖象過點![]() (3,0)、
(3,0)、![]() (-1,0).
(-1,0).
(1)求二次函數的解析式;
(2)如圖,二次函數的圖象與![]() 軸交于點
軸交于點![]() ,二次函數圖象的對稱軸與直線
,二次函數圖象的對稱軸與直線![]() 交于點
交于點![]() ,求
,求![]() 點的坐標;
點的坐標;
(3)在第一象限內的拋物線上有一點![]() ,當
,當![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD的邊長是2,E是DC上一點,△ADE經順時針旋轉后與△ABF重合.
(1)指出旋轉的中心和旋轉的角度;
(2)如果連結EF,那么△AEF是怎樣的三角形?請說明理由.
(3)已知點G在BC上,且∠GAE=45°.
① 試說明GE=DE+BG.
② 若E是DC的中點,求BG的長.
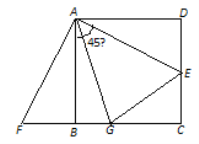
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com