
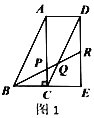
【題目】現有多個全等直角三角形,先取三個拼成如圖1所示的形狀,![]() 為
為![]() 的中點,
的中點,![]() 分別交
分別交![]() ,
,![]() 于
于![]() ,
,![]() ,易得
,易得![]() .若取四個直角三角形拼成如圖2所示的形狀,
.若取四個直角三角形拼成如圖2所示的形狀,![]() 為
為![]() 的中點,
的中點,![]() 分別交
分別交![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() ,則
,則![]() _________.
_________.
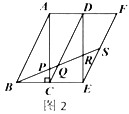
【答案】![]()
【解析】
首先證明△BCQ∽△BES,從而可求得CQ=![]() EF,DQ=
EF,DQ=![]() EF,然后證明△BAP∽△QDR得到BP:QR=4:3從而可知:BP:PQ:QR=4:1:3,然后由DQ∥SE,可知:QR:RS=DQ:SE=3:2,從而可求得BP:PQ:QR:RS=4:1:3:2.
EF,然后證明△BAP∽△QDR得到BP:QR=4:3從而可知:BP:PQ:QR=4:1:3,然后由DQ∥SE,可知:QR:RS=DQ:SE=3:2,從而可求得BP:PQ:QR:RS=4:1:3:2.
解:(1)∵四個直角三角形是全等三角形,
∴AB=EF=CD,AB∥EF∥CD,BC=CE,AC∥DE,
∴BP:PR=BC:CE=1,
∵CD∥EF,
∴△BCQ∽△BES.
又∵BC=CE
∴CQ=![]() SE=
SE=![]() EF,
EF,
∴DQ=![]() EF,
EF,
∵AB∥CD,
∴∠ABP=∠DQR.
又∵∠BAP=∠QDR,
∴△BAP∽△QDR.
∴BP:QR=4:3.
∴BP:PQ:QR=4:1:3,
∵DQ∥SE,
∴QR:RS=DQ:SE=3:2,
∴BP:PQ:QR:RS=4:1:3:2.
故答案為:4:1:3:2


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:初中數學 來源: 題型:
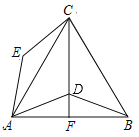
【題目】如圖,點D是等邊△ABC內一點,將線段AD繞著點A逆時針旋轉60°得到線段AE,連結CD并延長交AB于點F,連結BD,CE.
(1)求證:△ACE≌△ABD;
(2)當CF⊥AB時,∠ADB=140°,求∠ECD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 交x軸于點A(-3,0)和點B,交y軸于點C(0,3).
交x軸于點A(-3,0)和點B,交y軸于點C(0,3).
(1)求拋物線的函數表達式;
(2)若點Q是線段AC上的一動點,作DQ⊥x軸,交拋物線于點D,求線段DQ長度的最大值.
(3)點G是拋物線上的動點,點F在x軸上的動點,若以A,C,F,G四個點為頂點的四邊形是平行四邊形,求出所有滿足條件的點F坐標(直接寫出結果).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,四邊形
的直徑,四邊形![]() 是矩形,
是矩形,![]() 是
是![]() 上的點,
上的點,![]() ,與
,與![]() 交于點
交于點![]() ,己知
,己知![]() ,
,![]() 的半徑為30.
的半徑為30.
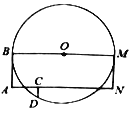
(1)求![]() 的長.
的長.
(2)連接![]() ,若將扇形
,若將扇形![]() 卷成一個圓錐,求這個圓錐底面半徑的長.
卷成一個圓錐,求這個圓錐底面半徑的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展“江山如此多嬌”為主題的地理知識競賽活動,要求每班派出一名同學代表本班參賽.九年一班四名同學主動報名,老師為了確定最終參賽人選,對這四名同學的歷次地理考試成績進行了匯總,數據如下:

班級里數學小組的同學對上面的數據進行了進一步的整理:

根據以上的信息,回答下列問題:
(1)寫出上表中![]() ,
,![]() ,
,![]() .
.
(2)丙同學看到統計表,對老師說:“我的成績方差最小,說明我的成績最穩定,應該派我去參賽!”請問你是否同意他的觀點?若你是老師,你將派誰參賽?說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市“上品”房地產開發公司于2010年5月份完工一商品房小區,6月初開始銷售,其中6月的銷售單價為0.7萬元![]() ,7月的銷售單價為0.72萬元
,7月的銷售單價為0.72萬元![]() ,且每月銷售價格
,且每月銷售價格![]() (單位:萬元
(單位:萬元![]() )與月份
)與月份![]() (
(![]() ,
,![]() 為整數)之間滿足一次函數關系:每月的銷售面積為
為整數)之間滿足一次函數關系:每月的銷售面積為![]() (單位:
(單位:![]() ),其中
),其中![]() .(
.(![]() ,
,![]() 為整數).
為整數).
(1)求![]() 與月份
與月份![]() 的函數關系式;
的函數關系式;
(2)6~11月中,哪一個月的銷售額最高?最高銷售額為多少萬元?
(3)2010年11月時,因會受到即將實行的“國八條”和房產稅政策的影響,該公司銷售部預計12月份的銷售面積會在11月銷售面積基礎上減少![]() ,于是決定將12月份的銷售價格在11月的基礎上增加
,于是決定將12月份的銷售價格在11月的基礎上增加![]() ,該計劃順利完成.為了盡快收回資金,2011年月公司進行降價促銷,該月銷售額為
,該計劃順利完成.為了盡快收回資金,2011年月公司進行降價促銷,該月銷售額為![]() 萬元.這樣12月、1月的銷售額共為4618.4萬元,請根據以上條件求出
萬元.這樣12月、1月的銷售額共為4618.4萬元,請根據以上條件求出![]() 的值為多少?
的值為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com