
【題目】如圖,在平面直角坐標系中,將△ABO繞點A順時針旋轉到△AB1C1的位置,點B、O分別落在點B1、C1處,點B1在x軸上,再將△AB1C1繞點B1順時針旋轉到△A1B1C2的位置,點C2在x軸上,將△A1B1C2繞點C2順時針旋轉到△A2B2C2的位置,點A2在x軸上,依次進行下去….若點A(![]() ,0),B(0,2),則點B2018的坐標為_____.
,0),B(0,2),則點B2018的坐標為_____.

【答案】(6054,2)
【解析】分析:
分析題意和圖形可知,點B1、B3、B5、……在x軸上,點B2、B4、B6、……在第一象限內,由已知易得AB=![]() ,結合旋轉的性質可得OA+AB1+B1C2=6,從而可得點B2的坐標為(6,2),同理可得點B4的坐標為(12,2),即點B2相當于是由點B向右平移6個單位得到的,點B4相當于是由點B2向右平移6個單位得到的,由此即可推導得到點B2018的坐標.
,結合旋轉的性質可得OA+AB1+B1C2=6,從而可得點B2的坐標為(6,2),同理可得點B4的坐標為(12,2),即點B2相當于是由點B向右平移6個單位得到的,點B4相當于是由點B2向右平移6個單位得到的,由此即可推導得到點B2018的坐標.
詳解:
∵在△AOB中,∠AOB=90°,OA=![]() ,OB=2,
,OB=2,
∴AB=![]() ,
,
∴由旋轉的性質可得:OA+AB1+B1C2=OA+AB+OB=6,C2B2=OB=2,
∴點B2的坐標為(6,2),
同理可得點B4的坐標為(12,2),
由此可得點B2相當于是由點B向右平移6個單位得到的,點B4相當于是由點B2向右平移6個單位得到,
∴點B2018相當于是由點B向右平移了:![]() 個單位得到的,
個單位得到的,
∴點B2018的坐標為(6054,2).
故答案為:(6054,2).


科目:初中數學 來源: 題型:
【題目】如圖,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD與BE相交于點P,則∠BPD的度數為( )
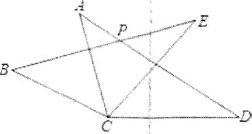
A. 120° B. 125° C. 130° D. 155°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=﹣ ![]() +bx+c的圖象經過A(2,0)、B(0,﹣6)兩點.
+bx+c的圖象經過A(2,0)、B(0,﹣6)兩點.
(1)求這個二次函數的解析式;
(2)設該二次函數的對稱軸與x軸交于點C,連接BA、BC,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年級(1)班開展了為期一周的“敬老愛親”社會活動,并根據學生做家務的時間來評價他們在活動中的表現,老師調查了全班50名學生在這次活動中做家務的時間,并將統計的時間(單位:小時)分成5組: A.0.5≤x<1 B.1≤x<1.5 C.1.5≤x<2 D.2≤x<2.5 E.2.5≤x<3;并制成兩幅不完整的統計圖(如圖):
請根據圖中提供的信息,解答下列問題:
(1)這次活動中學生做家務時間的中位數所在的組是;
(2)補全頻數分布直方圖;
(3)該班的小明同學這一周做家務2小時,他認為自己做家務的時間比班里一半以上的同學多,你認為小明的判斷符合實際嗎?請用適當的統計知識說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=3,AD=4,E為AB上一點,AE=1,M為射線AD上一動點,AM=a(a為大于0的常數),直線EM與直線CD交于點F,過點M作MG⊥EM,交直線BC于點G.
(1)若M為邊AD中點,求證△EFG是等腰三角形;
(2)若點G與點C重合,求線段MG的長;
(3)請用含a的代數式表示△EFG的面積S,并指出S的最小整數值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,梯子斜靠在與地面垂直(垂足為O)的墻上,當梯子位于AB位置時,它與地面所成的角∠ABO=60°;當梯子底端向右滑動1m(即BD=1m)到達CD位置時,它與地面所成的角∠CDO=51°18′,求梯子的長. (參考數據:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某數學興趣小組在數學課外活動中,研究三角形和正方形的性質時,做了如下探究:在△ABC中,∠BAC=90°,AB=AC,點D為直線BC上一動點(點D不與B,C重合),以AD為邊在AD右側作正方形ADEF,連接CF.
(1)觀察猜想
如圖①,當點D在線段BC上時。
①BC與CF的位置關系為:___;
②BC,CD,CF之間的數量關系為:___;(將結論直接寫在橫線上)
(2)數學思考
如圖②,當點D在線段CB的延長線上時,結論①,②是否仍然成立?若成立,請給予證明;若不成立,請你寫出正確結論再給予證明;
(3)拓展延伸
如圖③,當點D在線段BC的延長線上時,延長BA交CF于點G,連接GE.若已知AB=![]() ,CD=
,CD=![]() BC,請求出GE的長。
BC,請求出GE的長。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC中,AB=AC,∠BAC=90°.
(1)如圖(1),CD平分∠ACB交AB于點D,BE⊥CD于點E,延長BE、CA相交于點F,請猜想線段BE與CD的數量關系,并說明理由.
(2)如圖(2),點F在BC上,∠BFE=![]() ∠ACB,BE⊥FE于點E,AB與FE交于點D,FH∥AC交AB于H,延長FH、BE相交于點G,求證:BE=
∠ACB,BE⊥FE于點E,AB與FE交于點D,FH∥AC交AB于H,延長FH、BE相交于點G,求證:BE=![]() FD;
FD;
(3)如圖(3),點F在BC延長線上,∠BFE=![]() ∠ACB,BE⊥FE于點E,FE交BA延長線于點D,請你直接寫出線段BE與FD的數量關系(不需要證明).
∠ACB,BE⊥FE于點E,FE交BA延長線于點D,請你直接寫出線段BE與FD的數量關系(不需要證明).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com