
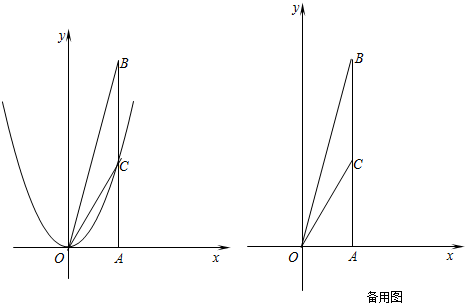
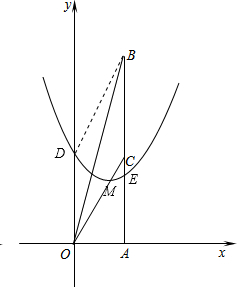
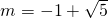 ,
,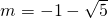 (舍去),
(舍去),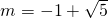
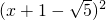 +2×(-1+
+2×(-1+ )
)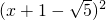 -2+2
-2+2 ,
, BE•OA
BE•OA (4+2m-m2)×2
(4+2m-m2)×2

 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:初中數學 來源: 題型:
 如圖,Rt△AOB中,AB⊥OB,且AB=OB=3,設直線x=t截此三角形所得陰影部分的面積為S,則S與t之間的函數關系的圖象為下列選項中的( )
如圖,Rt△AOB中,AB⊥OB,且AB=OB=3,設直線x=t截此三角形所得陰影部分的面積為S,則S與t之間的函數關系的圖象為下列選項中的( )A、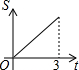 | B、 | C、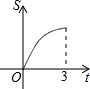 | D、 |
查看答案和解析>>
科目:初中數學 來源: 題型:
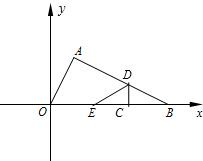 如圖在Rt△AOB中,∠BAO=90°,O為坐標原點,B在x軸正半軸上,A在第一象限.OA和AB的長是方程x2-3
如圖在Rt△AOB中,∠BAO=90°,O為坐標原點,B在x軸正半軸上,A在第一象限.OA和AB的長是方程x2-3| 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖在Rt△AOB中,∠BAO=90°,O為坐標原點,B在x軸正半軸上,A在第一象限,OA和AB的長是方程x2-3
如圖在Rt△AOB中,∠BAO=90°,O為坐標原點,B在x軸正半軸上,A在第一象限,OA和AB的長是方程x2-3| 5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com