【題目】如圖，拋物線y＝ax2+bx+c（a≠0）的對稱軸為直線x＝﹣2，與x軸的一個交點在（﹣3，0）和（﹣4，0）之間，其部分圖象如圖所示則下列結論：①4a﹣b＝0；②c＜0；③c＞3a；④4a﹣2b＞at2+bt（t為實數）；⑤點（﹣
，y1），（﹣
，y2），（
）是該拋物線上的點，則y2＜y1＜y3，其中，正確結論的個數是（ ）
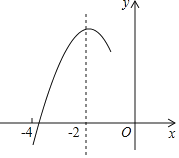
A. 1B. 2C. 3D. 4
【答案】C
【解析】
根據拋物線的對稱軸可判斷①；由拋物線與x軸的交點及拋物線的對稱性可判斷②；由x＝﹣1時y＞0可判斷③，由x＝﹣2時函數取得最大值可判斷④；根據拋物線的開口向下且對稱軸為直線x＝﹣2知圖象上離對稱軸水平距離越小函數值越大，可判斷⑤．
∵拋物線的對稱軸為直線x＝﹣2，
∴4a﹣b＝0，所以①正確；
∵與x軸的一個交點在（﹣3，0）和（﹣4，0）之間，
∴由拋物線的對稱性知，另一個交點在（﹣1，0）和（0，0）之間，
∴拋物線與y軸的交點在y軸的負半軸，即c＜0，故②正確；
∵由②知，x＝﹣1時y＞0，且b＝4a，
即a﹣b+c＝a﹣4a+c＝﹣3a+c＞0，
所以③正確；
由函數圖象知當x＝﹣2時，函數取得最大值，
∴4a﹣2b+c≥at2+bt+c，
即4a﹣2b≥at2+bt（t為實數），故④錯誤；
∵拋物線的開口向下，且對稱軸為直線x＝﹣2，
∴拋物線上離對稱軸水平距離越小，函數值越大，
∴y2＞y1＞y3，故⑤錯誤；
故選：C．
全優點練單元計劃系列答案科目：初中數學 來源： 題型：
【題目】現需了解2019年各月份中5至14日廣州市每天最低氣溫的情況：圖①是3月份的折線統計圖．（數據來源于114天氣網）
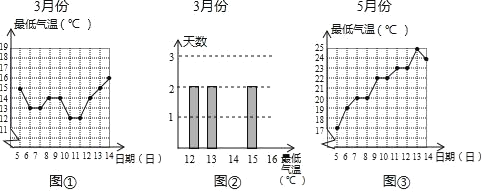
（1）圖②是3月份的頻數分布直方圖，根據圖①提供的信息，補全圖②中的頻數分布直方圖；
（2）3月13日與10日這兩天的最低氣溫之差是 ℃；
（3）圖③是5月份的折線統計圖．用
表示5月份的方差；用
表示3月份的方差，比較大小： ；比較3月份與5月份， 月份的更穩定．
查看答案和解析>>
科目：初中數學 來源： 題型：
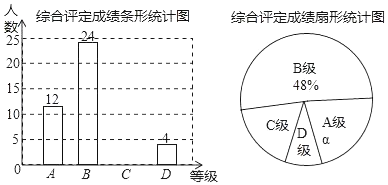
【題目】設中學生體質健康綜合評定成績為x分，滿分為100分，規定：85≤x≤100為A級，75≤x≤85為B級，60≤x≤75為C級，x＜60為D級．現隨機抽取某中學部分學生的綜合評定成績，整理繪制成如下兩幅不完整的統計圖，請根據圖中的信息，解答下列問題：
（1）在這次調查中，一共抽取了 名學生，α＝ %；
（2）補全條形統計圖；
（3）扇形統計圖中C級對應的圓心角為 度；
（4）若A級由2個男生參加自主考試，B級由1個女生參加自主考試，剛好有一男一女考取名校，請用樹狀圖或列表法求他們的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
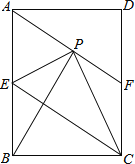
【題目】如圖，在矩形ABCD中，E是AB邊的中點，沿EC對折矩形ABCD，使B點落在點P處，折痕為EC，連接AP并延長AP交CD于F點，連接BP．
（1）求證：四邊形AECF為平行四邊形；
（2）若BC＝
AB，判斷△ABP的形狀，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
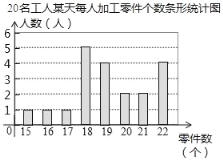
【題目】某部門為了解工人的生產能力情況，進行了抽樣調查．該部門隨機抽取了20名工人某天每人加工零件的個數，數據如下：整理上面數據，得到條形統計圖；樣本數據的平均數、眾數、中位數如表所示：
統計量 | 平均數 | 眾數 | 中位數 |
數值 | 19.2 | m | n |
根據以上信息，解答下列問題：
（1）上表中m、n的值分別為 ， ；
（2）為調動積極性，該部門根據工人每天加工零件的個數制定了獎勵標準，凡達到或超過這個標準的工人將獲得獎勵．如果想讓60%左右的工人能獲獎，應根據 來確定獎勵標準比較合適（填“平均數”、“眾數”或“中位數”）；
（3）該部門規定：每天加工零件的個數達到或超過21個的工人為生產能手若該部門有300名工人，試估計該部門生產能手的人數；
（4）現決定從小王、小張、小李、小劉中選兩人參加業務能手比賽，直接寫出恰好選中小張、小李兩人的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀材料：
小明在學習二次根式后，發現一些含根號的式子可以寫成另一個式子的平方，如
．善于思考的小明進行了以下探索：
設
（其中
、
、
、
均為整數），則有
．
，
．這樣小明就找到了一種把類似
的式子化為平方式的方法．
請你仿照小明的方法探索并解決下列問題：
（1）當、、、均為正整數時，若
，用含、的式子分別表示、，得：
，
；
（2）利用所探索的結論，找一組正整數、、、填空： 
；
（3）若
，且、、均為正整數，求的值？
查看答案和解析>>
科目：初中數學 來源： 題型：
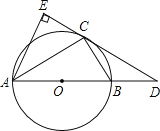
【題目】如圖，已知⊙O是△ABC的外接圓，AB是⊙O的直徑，點D是AB延長線上的一點，AE⊥DC交DC的延長線于點E，AC平分∠DAE．
（1）DE與⊙O有何位置關系？請說明理由．
（2）若AB=6，CD=4，求CE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合與實踐
（1）（探索發現）
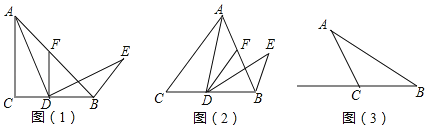
在△ABC中，AC＝BC，∠ACB＝a，點D為直線BC上一動點（點D不與點B，C重合），過點D作DF∥AC交直線AB于點F，將AD繞點D順時針旋轉a得到ED，連接BE，如圖（1），當點D在線段BC上，且a＝90°時，試猜想：
①AF與BE之間的數量關系： ；
②∠ABE＝ ．
（2）（拓展探究）
如圖（2），當點D在線段BC上，且0°＜a＜90°時，判斷AF與BE之間的數量關系及∠ABE的度數，請說明理由．
（3）（解決問題）
如圖（3），在△ABC中，AC＝BC，AB＝4，∠ACB＝a，點D在射線BC上，將AD繞點D順時針旋轉a得到ED，連接BE．當BD＝3CD時，請直接寫出BE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖在平行四邊形ABCD中，CD＝2AD，BE⊥AD，點F為DC中點，連接EF、BF，下列結論：①∠ABC＝2∠ABF；②EF＝BF；③S四邊形DEBC＝2S△EFB；④∠CFE＝3∠DEF，其中正確的有_____．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com