
【題目】如圖,在平面直角坐標系中,△AOB的頂點O為坐標原點,點A的坐標為(4,0),點B的坐標為(0,1),點C為邊AB的中點,正方形OBDE的頂點E在x軸的正半軸上,連接CO,CD,CE.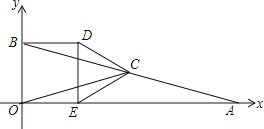
(1)線段OC的長為;
(2)求證:△CBD≌△COE;
(3)將正方形OBDE沿x軸正方向平移得到正方形O1B1D1E1 , 其中點O,B,D,E的對應點分別為點O1 , B1 , D1 , E1 , 連接CD,CE,設點E的坐標為(a,0),其中a≠2,△CD1E1的面積為S.
①當1<a<2時,請直接寫出S與a之間的函數表達式;
②在平移過程中,當S= ![]() 時,請直接寫出a的值.
時,請直接寫出a的值.
【答案】
(1)![]()
(2)
證明:∵∠AOB=90°,點C是AB的中點,
∴OC=BC= ![]() AB,
AB,
∴∠CBO=∠COB,
∵四邊形OBDE是正方形,
∴BD=OE,∠DBO=∠EOB=90°,
∴∠CBD=∠COE,
在△CBD和△COE中,
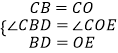 ,
,
∴△CBD≌△COE(SAS)
(3)
解:①解:過點C作CH⊥D1E1于點H,
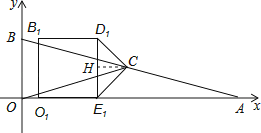
∵C是AB邊的中點,
∴點C的坐標為:(2, ![]() )
)
∵點E的坐標為(a,0),1<a<2,
∴CH=2﹣a,
∴S= ![]() D1E1CH=
D1E1CH= ![]() ×1×(2﹣a)=﹣
×1×(2﹣a)=﹣ ![]() a+1;
a+1;
②當1<a<2時,S=﹣ ![]() a+1=
a+1= ![]() ,
,
解得:a= ![]() ;
;
當a>2時,同理:CH=a﹣2,
∴S= ![]() D1E1CH=
D1E1CH= ![]() ×1×(a﹣2)=
×1×(a﹣2)= ![]() a﹣1,
a﹣1,
∴S= ![]() a﹣1=
a﹣1= ![]() ,
,
解得:a= ![]() ,
,
綜上可得:當S= ![]() 時,a=
時,a= ![]() 或
或 ![]() .
.
【解析】解:(1)∵點A的坐標為(4,0),點B的坐標為(0,1),
∴OA=4,OB=1,
∵∠AOB=90°,
∴AB= ![]() =
= ![]() ,
,
∵點C為邊AB的中點,
∴OC= ![]() AB=
AB= ![]() ;故答案為:
;故答案為: ![]() .
.
(1)由點A的坐標為(4,0),點B的坐標為(0,1),利用勾股定理即可求得AB的長,然后由點C為邊AB的中點,根據直角三角形斜邊的中線等于斜邊的一半,可求得線段OC的長;(2)由四邊形OBDE是正方形,直角三角形斜邊的中線等于斜邊的一半,易得BD=OE,BC=OC,∠CBD=∠COE,即可證得:△CBD≌△COE;(3)①首先根據題意畫出圖形,然后過點C作CH⊥D1E1于點H,可求得△CD1E1的高與底,繼而求得答案;
②分別從1<a<2與a>2去分析求解即可求得答案. 此題屬于四邊形的綜合題.考查了正方形的性質、直角三角形的性質、勾股定理、全等三角形的判定與性質以及三角形面積問題.注意掌握輔助線的作法,注意掌握分類討論思想的應用是解此題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖的七邊形ABCDEFG中,AB、ED的延長線相交于O點.若圖中∠1、∠2、∠3、∠4的外角的角度和為220°,則∠BOD的度數是( )

A. 400 B. 450 C. 500 D. 600
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD對角線交于點O,BE∥AC,AE∥BD,EO與AB交于點F.
(1)試判斷四邊形AEBO的形狀,并說明你的理由;
(2)求證:EO=DC.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了傳承優秀傳統文化,某校開展“經典誦讀”比賽活動,誦讀材料有《論語》,《三字經》,《弟子規》(分別用字母A,B,C依次表示這三個誦讀材料),將A,B,C這三個字母分別寫在3張完全相同的不透明卡片的正面上,把這3張卡片背面朝上洗勻后放在桌面上.小明和小亮參加誦讀比賽,比賽時小明先從中隨機抽取一張卡片,記錄下卡片上的內容,放回后洗勻,再由小亮從中隨機抽取一張卡片,選手按各自抽取的卡片上的內容進行誦讀比賽.
(1)小明誦讀《論語》的概率是;
(2)請用列表法或畫樹狀圖(樹形圖)法求小明和小亮誦讀兩個不同材料的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場服裝部分為了解服裝的銷售情況,統計了每位營業員在某月的銷售額(單位:萬元),并根據統計的這組銷售額的數據,繪制出如下的統計圖①和圖②.請根據相關信息,解答下列問題:
該商場服裝營業員的人數為 ,圖①中m的值為 ;
求統計的這組銷售額數據的平均數、眾數和中位數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的小正方形組成的6![]() 6網格中,A,B,C是格點(我們把組成網格的小正方形的頂點,稱為格點),其中點C在直線AB外。
6網格中,A,B,C是格點(我們把組成網格的小正方形的頂點,稱為格點),其中點C在直線AB外。
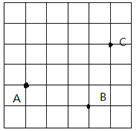
(1)過A點畫AB的垂線AG;
(2)過C點畫AB的平行線CH;
(3)連接BC,線段BC與線段AB的關系:______________;
(4)_____________________是點C到直線AB的距離;
(5)因為直線外一點和直線上各點連接的所有線段中,垂線段最短,所以線段AC,BC的大小關系是______________(用“<”號連接)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知a、b、c滿足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判斷以a、b、c為邊能否構成三角形?若能構成三角形,此三角形是什么形狀?并求出三角形的面積;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABO的頂點O在坐標原點,點B在x軸上,∠ABO=90°,∠AOB=30°,OB=2 ![]() ,反比例函數y=
,反比例函數y= ![]() (x>0)的圖象經過OA的中點C,交AB于點D.
(x>0)的圖象經過OA的中點C,交AB于點D. 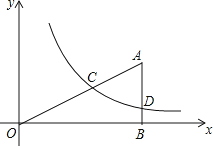
(1)求反比例函數的關系式;
(2)連接CD,求四邊形CDBO的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,內部有6個全等的正方形,小正方形的頂點E、F、G、H分
別在邊AD、AB、BC、CD上,則tan∠DEH=( )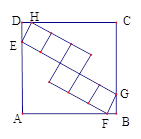
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com