
【題目】如圖,直線AB交x軸于點A(4,0),交y軸于點B,交反比例函數y=![]() (k≠0)于點P(第一象限),若點P的縱坐標為2,且tan∠BAO=1
(k≠0)于點P(第一象限),若點P的縱坐標為2,且tan∠BAO=1
(1)求出反比例函數y=![]() (k≠0)的解析式;
(k≠0)的解析式;
(2)過線段AB上一點C作x軸的垂線,交反比例函數y=![]() (k≠0)于點D,連接PD,當△CDP為等腰三角形時,求點C的坐標.
(k≠0)于點D,連接PD,當△CDP為等腰三角形時,求點C的坐標.
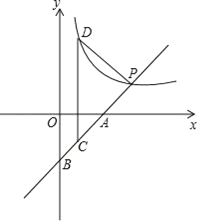
【答案】(1)y=![]() (2)當C(2,-2)時,△CDP為等腰直角三角形
(2)當C(2,-2)時,△CDP為等腰直角三角形
【解析】試題分析:(1)過P作PE⊥x軸于點E,求出點P的坐標,進而求出反比例函數的解析式;
(2)首先求出直線AB的解析式,然后設C(m,m-4),則D(m, ![]() ),過P作PF⊥CD于F.則F(m,2),則F(m,2),根據DF=CF列出m的方程求出m即可.
),過P作PF⊥CD于F.則F(m,2),則F(m,2),根據DF=CF列出m的方程求出m即可.
試題解析:(1)過P作PE⊥x軸于點E,∵tan∠BAO=1,∴∠BAO=45°,
∴∠BAO=∠ABO=∠PAE=45°
∵點P的縱坐標為2,∴PE=AE=2,∵A(4,0),∴P(6,2)
把點P代人y=![]() 得k=12.∴反比例函數的解析式為y=
得k=12.∴反比例函數的解析式為y=![]()
(2)設直線AB的解析式為y=kx+b且過A(4,0),P(6,2)
![]() ,解得
,解得![]() ,∴y=x-4
,∴y=x-4
要使△CDP是等腰直角三角形,只能∠DPC=90°,
設C(m,m-4),則D(m, ![]() ).過P作PF⊥CD于F.則F(m,2),
).過P作PF⊥CD于F.則F(m,2),
∴PD=PC,PF⊥CD,∴DF=CF,∴![]() -2=2-(m-4),
-2=2-(m-4),
∴m2-8m+12=0,(m-2)(m-6)=0,∴m1=2,m2=6(不合題意,舍去),
∴當C(2,-2)時,△CDP為等腰直角三角形。


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
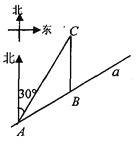
【題目】如圖,某市郊外景區內一條筆直的公路a經過A、B兩個景點,景區管委會又開發了風景優美的景點C,經測量景點C位于景點A的北偏東30°方向8km處,位于景點B的正北方向,已知AB=5km.
(1)求景點B與景點為C的距離;(結果保留根號)
(2)為方便游客到景點游玩,景區管委會準備由景點C向公路a修建一條距離最短的公路,不考慮其它因素,求出這條公路的長.(結果精確到0.1km.參考數據: ![]() =1.73,
=1.73, ![]() =2.24)
=2.24)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是根據寶塔山公園的平面示意圖建立的平面直角坐標系,公園的入口位于坐標原點O,古塔位于點A(﹣400,300),從古塔出發沿射線OA方向前行300m是盆景園B,從盆景園B向右轉90°后直行400m到達櫻花園C,則點C的坐標是 . 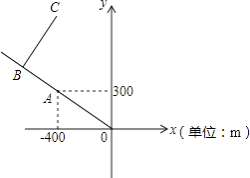
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=x2﹣(m+2)x+3(m﹣1)與x軸的兩個交點為A、B,與y軸交于點C,點D為拋物線的頂點,直線y=﹣2x+m+6經過點B,交y軸于點E(0,6).
(1)求直線和拋物線的解析式;
(2)如果拋物線的對稱軸與線段BC交于點H,且直線y=x與直線y=﹣2x+m+6交于點G,求證:四邊形OHBG是平行四邊形;
(3)在拋物線上是否存在點P,使△APB的面積等于平行四邊形OHBG的面積,若存在,直接寫出P點的坐標,若不存在請說明理由.
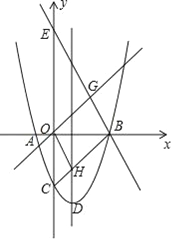
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解大氣污染情況,某學校興趣小組搜集了20I7年上半年中120天鄭州市的空氣質量指數,繪制了如下不完整的統計圖表:
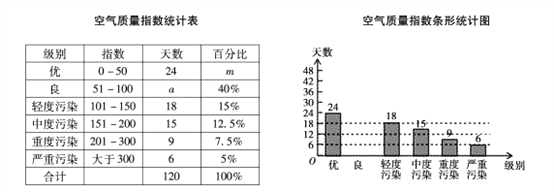
請根據圖表中提供的信息,解答下面的問題:
(1)空氣質量指數統計表中的a=_________,m=_________;
(2)請把空氣質量指數條形統計圖補充完整;
(3)若繪制“空氣質量指數扇形統計圖”,級別為“優”所對應扇形的圓心角是_________。
(4)請通過計算估計鄭州市2017年(365)天沖空氣質量指數大于100的天數。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC≌△DCB,若BC=10cm,AB=6cm,AC=7cm,則CD為( )
A. 10cm B. 7cm C. 6cm D. 6cm或7cm
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com