
【題目】如圖,O為矩形ABCD對角線的交點,DE∥AC,CE∥BD.
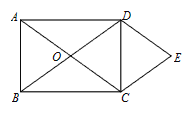
(1)試判斷四邊形OCED的形狀,并說明理由;
(2)若AB=6,BC=8,求四邊形OCED的面積.
【答案】(1)四邊形OCED是菱形.(2)24.
【解析】
試題分析:(1)首先可根據DE∥AC、CE∥BD判定四邊形ODEC是平行四邊形,然后根據矩形的性質:矩形的對角線相等且互相平分,可得OC=OD,由此可判定四邊形OCED是菱形.
(2)連接OE,通過證四邊形BOEC是平行四邊形,得OE=BC;根據菱形的面積是對角線乘積的一半,可求得四邊形ODEC的面積.
試題解析:(1)四邊形OCED是菱形.
∵DE∥AC,CE∥BD,
∴四邊形OCED是平行四邊形,
又在矩形ABCD中,OC=OD,
∴四邊形OCED是菱形.
(2)連接OE.由菱形OCED得:CD⊥OE,

又∵BC⊥CD,
∴OE∥BC(在同一平面內,垂直于同一條直線的兩直線平行),
又∵CE∥BD,
∴四邊形BCEO是平行四邊形;
∴OE=BC=8
∴S四邊形OCED=![]() OECD=
OECD=![]() ×8×6=24.
×8×6=24.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形![]() 中,以
中,以![]() 為直徑作半圓,
為直徑作半圓,![]() .現有兩動點
.現有兩動點![]() 、
、![]() ,分別從點
,分別從點![]() 、點
、點![]() 同時出發,點
同時出發,點![]() 沿線段
沿線段![]() 以
以![]() /秒的速度向點
/秒的速度向點![]() 運動,點
運動,點![]() 沿折線
沿折線![]() 以
以![]() /秒的速度向點
/秒的速度向點![]() 運動.當點
運動.當點![]() 到達
到達![]() 點時,
點時,![]() 、
、![]() 同時停止運動,設點
同時停止運動,設點![]() 運動時間為
運動時間為![]() .
.

(1)當![]() 為何值時,線段
為何值時,線段![]() 與
與![]() 平行?
平行?
(2)設![]() ,當
,當![]() 為何值時,
為何值時,![]() 與半圓相切?
與半圓相切?
(3)如圖2,將圖形放在直角坐標系中,當![]() 時,設
時,設![]() 與
與![]() 相交于點
相交于點![]() ,雙曲線
,雙曲線![]() 經過點
經過點![]() ,并且與邊
,并且與邊![]() 交于點
交于點![]() ,求出雙曲線的函數關系式,并直接寫出
,求出雙曲線的函數關系式,并直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標平面內,二次函數圖象的頂點為A(1,﹣4),且過點B(3,0).
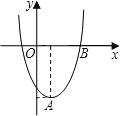
(1)求該二次函數的解析式;
(2)將該二次函數圖象向右平移幾個單位,可使平移后所得圖象經過坐標原點?并直接寫出平移后所得圖象與x軸的另一個交點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場購進一批單價為4元的日用品.若按每件5元的價格銷售,每月能賣出300件;若按每件6元的價格銷售,每月能賣出200件,假定每月銷售件數![]() (件)與價格
(件)與價格![]() (元/件)之間滿足一次函數關系.
(元/件)之間滿足一次函數關系.
(1)、試求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)、當銷售價格定為多少時,才能使每月的利潤最大?每月的最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com