如圖,在半徑為13的⊙O中,OC垂直弦AB于點B,交⊙O于點C,AB=24,則CD的長是
▲ .
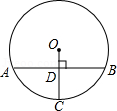
垂徑定理,勾股定理。
連接OA,
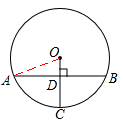
∵OC⊥AB,AB=24,∴AD=
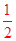
AB=12,
在Rt△AOD中,∵OA=13,AD=12,
∴
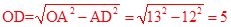
。
∴CD=OC﹣OD=13﹣5=8。
練習冊系列答案
相關習題
科目:初中數(shù)學
來源:不詳
題型:單選題
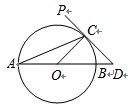
如圖,AB為⊙O的直徑,PD切⊙O于點C,交AB的延長線于D,且CO=CD,則
∠ACP=( )
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:單選題
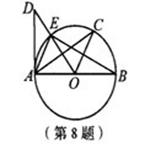
如圖,已知
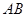
為
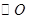
的直徑,
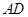
切
于點A,
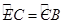
則下列結(jié)論不一定正確的是
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:填空題
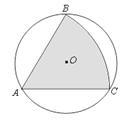
圖,有一直徑為4的圓形鐵皮,要從中剪出一個最大圓心角為60°的扇形ABC.那么剪下的扇形ABC(陰影部分)的面積為
;用此剪下的扇形鐵皮圍成一個圓錐,該圓錐的底面圓的半徑
r= .
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:單選題
如圖,點A、B、C在⊙O上,∠ABC=30°,則∠OAC等于
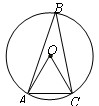
A.60° B.45° C.35° D.30°
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:解答題
如圖,在
中,
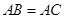
,以
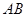
為直徑的⊙
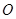
分別交
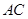
、
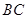
于點
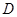
、
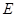
,點
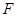
在
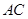
的延長線上,且
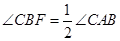
.
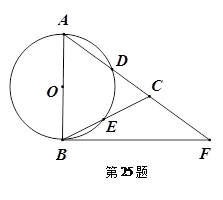
小題1:求證:直線
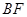
是⊙
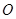
的切線;
小題2:若

,
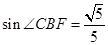
,求
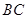
的長.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:單選題
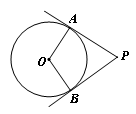
如圖,
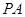
、
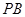
是⊙
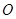
的切線,切點是
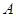
、
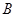
,已知
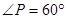
,
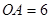
,那么
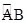
的弧長為( ).
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:填空題
若兩圓半徑分別為3和5,且圓心距為8,則兩圓位置關系為
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:填空題
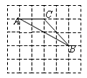
如圖,網(wǎng)格的小正方形的邊長均為1,小正方形的頂點叫做格點.
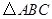
的三個頂點都在格點上,那么
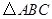
的外接圓半徑是
查看答案和解析>>


