
【題目】如圖(1),在□ABCD中,P是CD邊上的一點,AP與BP分別平分∠DAB和∠CBA。
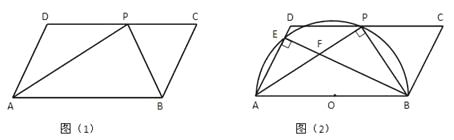
【1】判斷△APB是什么三角形?證明你的結論;
【2】比較DP與PC的大小;
【3】如圖(2)以AB為直徑作半圓O,交AD于點E,連結BE與AP交于點F,若AD=5cm,AP=8cm,求證△AEF∽△APB,并求tan∠AFE的值。
【答案】
【1】 △APB是直角三角形,理由如下:
∵在□ABCD中,AD∥BC,
∴∠DAB +∠ABC = 180°;
又∵AP與BP分別平分∠DAB和∠CBA,
∴∠PAB =![]() ,∠PBA =
,∠PBA =![]() ,
,
∴∠PAB+∠PBA=![]() ,
,
∴△APB是直角三角形;
【2】 ∵DC∥AB,
∴∠BAP =∠DPA.
∵∠DAP =∠PAB,
∴∠DAP =∠DPA,
∴DA = DP
同理證得CP=CB.
∴DP = PC
【3】 ∵AB是⊙O直徑,
∴∠AEB = 90°.
又(1)易知∠APB = 90°.
∴∠AEB =∠APB,
∵AP為角平分線,即∠EAF=∠PAB,
∴△AEF∽△APB,
由(2)可知DP =" PC" = AD,
∴ AB =" DC" =" 2AD" = 10cm,
在Rt△PAB中,![]() (cm)
(cm)
又△AEF∽△APB,
得∠AFE=∠ABP,
∴tan∠AFE = tan∠ABP=![]() 。
。
【解析】
【1】可通過角的度數來判斷三角形APB的形狀.由于ABCD是平行四邊形,AD∥BC,那么同旁內角∠DAB和∠CBA的和應該是180°,AP,BE平分∠DAB,∠ABP,于是∠PAB和∠ABP的和就應該是90°,即∠APB=90°,因此可得出三角形APB的形狀.
【2】可通過平行和角平分線,通過等角對等邊得出DP=AP,同理可證出PC=BC,根據平行四邊形的性質,AD=BC,可得出DP=PC.
【3】利用兩個角相等求出△AEF∽△APB,然后利用(2)求出PB的長度,在根據∠AFE=∠ABP,然后求出tan∠AFE的值.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:初中數學 來源: 題型:
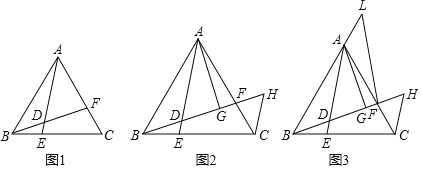
【題目】△ABC是等邊三角形,點E、F分別是邊BC、AC上的點,且BE=CF,AE、BF交于點D.
(1)如圖1,求證:AE=BF.
(2)如圖2,過點A作AG⊥BF于點G,過點C作CH∥AE交BF延長線于點H,若D為BG中點,求BH:CH的值;
(3)如圖3,在(2)的條件下,L為BA延長線上一點,且FL=FB,△FLA的面積為2,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O的內接四邊形ABCD中,AB=AD,∠C=120°,點E在⊙O上.
(1)求∠AED的度數;
(2)若⊙O的半徑為2,則![]() 的長為多少?
的長為多少?
(3)連接OD,OE,當∠DOE=90°時,AE恰好是⊙O的內接正n邊形的一邊,求n的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
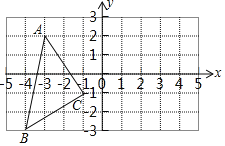
【題目】如圖,在平面直角坐標系中,△ABC的頂點A、B、C坐標分別為(﹣3,2),(﹣4,﹣3),(﹣1,﹣1).
(1)畫出△ABC關于y軸對稱的△A1B1C1;(A、B、C的對稱點分別為A1、B1、C1)
(2)寫出△A1B1C1各頂點A1、B1、C1的坐標.A1 、B1 、C1
(3)直接寫出△ABC的面積= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明在學習二次根式后,發現一些含根號的式子可以寫成另一個式子的平方,如:3+2![]() ,善于思考的小明進行了以下探索:
,善于思考的小明進行了以下探索:
設a+b![]() (其中a、b、m、n均為整數),
(其中a、b、m、n均為整數),
則有:a+b![]() ,∴a=m2+2n2,b=2mn,這樣小明就找到了一種把類似a+b
,∴a=m2+2n2,b=2mn,這樣小明就找到了一種把類似a+b![]() 的式子化為平方式的方法.
的式子化為平方式的方法.
請你仿照小明的方法探索并解決下列問題:
(1)當a、b、m、n均為正整數時,若a+b![]() ,用含m、n的式子分別表示a、b得:a= ,b= ;
,用含m、n的式子分別表示a、b得:a= ,b= ;
(2)利用所探索的結論,用完全平方式表示出:7+4![]() = .
= .
(3)請化簡:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
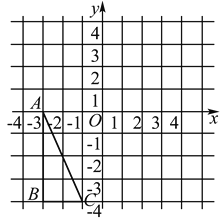
【題目】在平面直角坐標系中,△ABC的三個頂點坐標分別為A(-3,0),B(-3,-4),C(-1,-4).
(1)求△ABC的面積;
(2)在圖中作出△ABC關于x軸對稱的圖形△DEF,點A、B、C的對稱點分別為D、E、F,并寫出D、E、F的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD與CE交于點F,∠ACE=45°.
(1)求證:BE=EF;
(2)如圖2,G在BC的延長線上,連接GA,若GA=GB,求證:AC平分∠DAG;
(3)如圖3,在(2)的條件下,H為AG的中點,連接DH交AC于M,連接EM、ED,若S△EMC=4,∠BAD=15°,求AM的長.
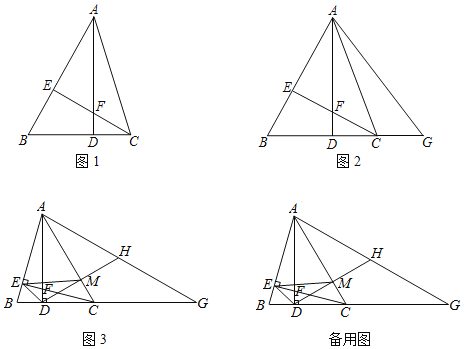
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.若 a、b、c是△ABC的三邊,則a2+b2=c2
B.若 a、b、c是Rt△ABC的三邊,則a2+b2=c2
C.若 a、b、c是Rt△ABC的三邊,![]() ,則a2+b2=c2
,則a2+b2=c2
D.若 a、b、c是Rt△ABC的三邊,![]() ,則a2+b2=c2
,則a2+b2=c2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com