
【題目】![]() 問題發現
問題發現
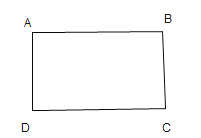
如圖![]() ,正方形
,正方形![]() 將正方形
將正方形![]() 繞點
繞點![]() 旋轉,直線
旋轉,直線![]() 交于點
交于點![]() 請直接寫出線段
請直接寫出線段![]() 與
與![]() 的數量關系是 ,位置關系是 _;
的數量關系是 ,位置關系是 _;
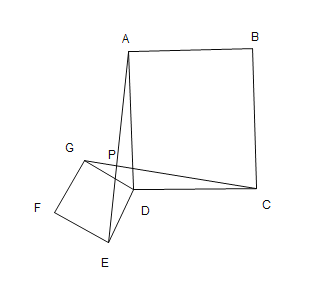
![]() 拓展探究
拓展探究
如圖![]() ,矩形
,矩形![]() 將矩形
將矩形![]() 繞點
繞點![]() 旋轉,直線
旋轉,直線![]() 交于點
交于點![]()
![]() 中線段關系還成立嗎/若成立,請寫出理由;若不成立,請寫出線段
中線段關系還成立嗎/若成立,請寫出理由;若不成立,請寫出線段![]() 的數量關系和位置關系,并說明理由;
的數量關系和位置關系,并說明理由;
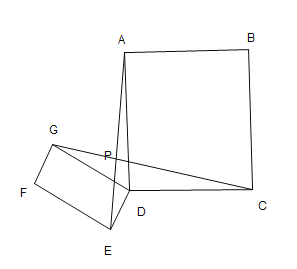
![]() 解決問題
解決問題
在![]() 的條件下,
的條件下,![]() 矩形
矩形![]() 繞
繞![]() 點旋轉過程中,請直接寫出當點
點旋轉過程中,請直接寫出當點![]() 與點
與點![]() 重合時,線段
重合時,線段![]() 的長,
的長,
【答案】![]() ;
;![]() 中數量關系不成立,位置關系成立.
中數量關系不成立,位置關系成立.![]() ,理由見解析;
,理由見解析;![]() 或
或![]()
【解析】
(1)證明△ADE≌△CDG(SAS),可得AE=CG,∠DAG=∠DCG,再由直角三角形兩個銳角互余即可證得AE⊥CG;
(2)先證明△ADE∽△CDG,利用相似三角形的性質證明即可.
(3)先通過作圖找到符合題意的兩種情況,第一種情況利用勾股定理求解即可;第二種情況借助相似三角形及勾股定理計算即可.
(1)![]() ;
;
理由如下:由題意知在正方形![]() 中,
中,
![]() ,
,![]() ,
,
![]()
![]()
在△ADE與△CDG中,
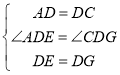
∴△ADE≌△CDG(SAS)
∴![]() ,
,![]()
∵對頂角相等,
∴![]()
![]()
![]() .
.
(2)(1)中數量關系不成立,位置關系成立.即:![]()
理由如下:
由題意知在矩形![]() 中,
中,![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,![]()
∵對頂角相等
∴![]()
![]()
![]() .
.
綜上所述:![]()
(3)
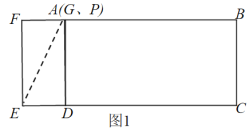
如圖1,當點G、P在點A處重合時,連接AE,
則此時∠ADE=∠GDE=90°
∴在Rt△ADE中,AE=![]() ,
,
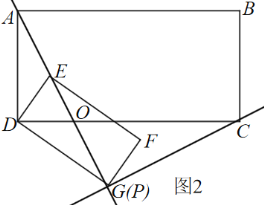
如圖1,當點G、P重合時, 則點A、E、G在同一直線上,
∵AD=DG=4,
∴∠DAG=∠DGA,
∵∠ADC=∠AGP=90°,∠AOD=∠COG,
∴∠DAG=∠COG,
∴∠DGA=∠COG,
又∵∠GDO=∠CDG,
∴△GDO∽△CDG,
∴![]()
∴![]()
∴DO=2,CG=2OG,
∴OC=DC-DO=8-2=6,
∵在Rt△COG中,OG2+GC2=OC2,
∴OG2+(2OG)2=62,
∴OG=![]() (舍負),
(舍負),
∴CG=![]() ,
,
由(2)得:![]()
∴AE=![]() ,
,
綜上所述,AE的長為![]() 或
或![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
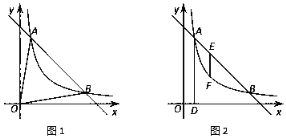
【題目】如圖1,點A(m,6),B(6,1)在反比例函數圖象上,作直線AB,連接OA、OB.
(1)求反比例函數的表達式和m的值;
(2)求△AOB的面積;
(3)如圖2,E是線段AB上一點,作AD⊥x軸于點D,過點E作x軸的垂線,交反比例函數圖象于點F,若EF=![]() AD,求出點E的坐標.
AD,求出點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 與直線
與直線![]() 有兩個不同的交點.下列結論:①
有兩個不同的交點.下列結論:①![]() ;②當
;②當![]() 時,
時,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有兩個不等實根;④若連接這兩個交點與拋物線的頂點,恰好是一個等腰直角三角形,則
有兩個不等實根;④若連接這兩個交點與拋物線的頂點,恰好是一個等腰直角三角形,則![]() ;其中正確的結論的個數是( )
;其中正確的結論的個數是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年中國北京世界園藝博覽會已于2019年4月29日在北京市延慶區開展,吸引了大批游客參觀游覽.五一小長假期間平均每天入園人數大約是8萬人,佳佳等5名同學組成的學習小組,隨機調查了五一假期中入園參觀的部分游客,獲得了他們在園內參觀所用時間,并對數據進行整理,描述和分析,下面給出了部分信息:
a.參觀時間的頻數分布表如下:
時間 | 頻數(人數) | 頻率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合計 |
| 1.000 |
b.參觀時間的頻數分布直方圖如圖:
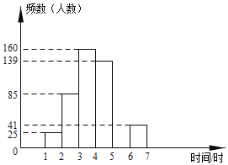
根據以上圖表提供的信息,解答下列問題:
(1)這里采用的調查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并請補全頻數分布直方圖;
(4)請你估算五一假期中平均每天參觀時間小于4小時的游客約有多少萬人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:點![]() 和
和![]() 是一次函數
是一次函數![]() 與反比例函數
與反比例函數![]() 圖象的兩個不同交點,點
圖象的兩個不同交點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,直線
,直線![]() 以及
以及![]() 分別與
分別與![]() 軸交與點
軸交與點![]() 和點
和點![]() .
.
(1)求反比例函數![]() 的表達式;
的表達式;
(2)若![]() ,求
,求![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:∠BAC.
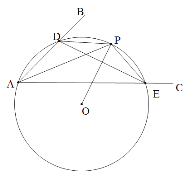
(1)如圖,在平面內任取一點O;
(2)以點O為圓心,OA為半徑作圓,交射線AB于點D,交射線AC于點E;
(3)連接DE,過點O作線段DE的垂線交⊙O于點P;
(4)連接AP,DP和PE.根據以上作圖過程及所作圖形,下列四個結論中:
①△ADE是⊙O的內接三角形; ② ![]() ;
;
③ DE=2PE; ④ AP平分∠BAC.
所有正確結論的序號是______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
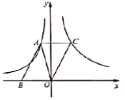
【題目】如圖,在平而直角坐標系![]() 中,函數
中,函數![]() (其中
(其中![]() ,
,![]() )的圖象經過平行四邊形
)的圖象經過平行四邊形![]() 的頂點
的頂點![]() ,函數
,函數![]() (其中
(其中![]() )的圖象經過頂點
)的圖象經過頂點![]() ,點
,點![]() 在
在![]() 軸上,若點
軸上,若點![]() 的橫坐標為1,
的橫坐標為1,![]() 的面積為
的面積為![]() .
.
(1)求![]() 的值:
的值:
(2)求直線![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系內,二次函數![]() 與一次函數
與一次函數![]() (a,b為常數,且
(a,b為常數,且![]() ).
).
(1)若y1,y2的圖象都經過點(2,3),求y1,y2的表達式;
(2)當y2經過點![]() 時,y1也過A,B兩點:
時,y1也過A,B兩點:
①求m的值;
②![]() 分別在y1,y2的圖象上,實數t使得“當
分別在y1,y2的圖象上,實數t使得“當![]() 或
或![]() 時,
時,![]() ”,試求t的最小值.
”,試求t的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com