
【題目】如圖,Rt△ABC中,∠ACB=90°,AC=3,BC=4,將邊AC沿CE翻折,使點A落在AB上的點D處;再將邊BC沿CF翻折,使點B落在CD的延長線上的點B′處,兩條折痕與斜邊AB分別交于點E、F,則線段B′F的長為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】首先根據折疊可得CD=AC=3,BC=4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,然后求得△BCF是等腰直角三角形,進而求得∠B/GD=90°,CE-EF=![]() ,ED=AE=
,ED=AE=![]() ,
,
從而求得B/D=1,DF=![]() ,在Rt△B/DF中,由勾股定理即可求得B/F的長.
,在Rt△B/DF中,由勾股定理即可求得B/F的長.
解:根據首先根據折疊可得CD=AC=3,B/C=B4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,
∴BD=4-3=1,∠DCE+∠B/CF=∠ACE+∠BCF,
∴∠ACB=90°,∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B/FC=135°,
∴∠B/FD=90°,
∵S△ABC=![]() AC×BC=
AC×BC=![]() AB×CE,
AB×CE,
∴AC×BC=AB×CE,
∵根據勾股定理求得AB=5,
∴CE=![]() ,∴EF=
,∴EF=![]() ,ED=AE=
,ED=AE=![]() =
=![]()
∴DE=EF-ED=![]() ,
,
∴B/F=![]() =
=![]() .
.
故答案為: ![]()
“點睛”此題主要考查了翻折變換,等腰三角形的判定和性質,勾股定理的應用等,根據折疊的性質求得相等的角是解本題的關鍵.


科目:初中數學 來源: 題型:
【題目】今年4月初,某地連續降雨導致該地某水庫水位持續上漲,下表是該水庫4月1日~4月4日的水位變化情況:
日期x | 1 | 2 | 3 | 4 |
水位y(米) | 20.0 | 20.5 | 21.0 | 21.5 |
(1)請建立該水庫水位y(米)與日期x之間的函數模型,求出函數表達式;
(2)請用求出的函數表達式預測該水庫今年4月6日的水位;
(3)你能用求出的函數表達式預測該水庫今年12月1日的水位嗎?請簡要說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
(1)如圖①.當∠COD在∠AOB的內部時
①若∠AOC=39°40′,求∠DOE的度數;
②若∠AOC=α,求∠DOE的度數(用含α的代數式表示),
(2)如圖②,當∠COD在∠AOB的外部時,
①請直接寫出∠AOC與∠DOE的度數之間的關系;
②在∠AOC內部有一條射線OF,滿足∠AOC+2∠BOE=4∠AOF,寫出∠AOF與∠DOE的度數之間的關系.
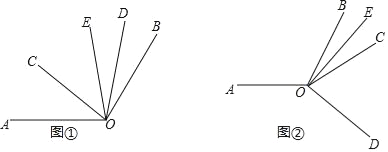
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一張矩形紙板按圖中虛線裁剪成九塊,其中有兩塊是邊長都為![]() 的大正方形,兩塊是邊長都為
的大正方形,兩塊是邊長都為![]() 的小正方形,五塊是長為
的小正方形,五塊是長為![]() 、寬為
、寬為![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上長度單位:cm)
.(以上長度單位:cm)
(1)觀察圖形,可以發現代數式![]() 可以因式分解為 ;
可以因式分解為 ;
(2)若每塊小矩形的面積為10![]() ,四個正方形的面積和為58
,四個正方形的面積和為58![]() ,試求圖中所有裁剪線(虛線部分)長之和.
,試求圖中所有裁剪線(虛線部分)長之和.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了進行資源的再利用,學校準備針對庫存的桌椅進行維修,現有甲、乙兩木工組,甲每天修桌凳14 套,乙每天比甲多7套,甲單獨修完這些桌凳比乙單獨修完多用20天.學校每天付甲組80元修理費,付乙組120元修理費.
(1)請問學校庫存多少套桌凳?
(2)在修理過程中,學校要派一名工人進行質量監督,學校負擔他每天10元生活補助費,現有三種修理方案:①由甲單獨修理;②由乙單獨修理;③甲、乙合作同時修理.你選哪種方案,為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
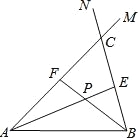
【題目】在線段AB的同側作射線AM和BN,若∠MAB與∠NBA的平分線分別交射線BN,AM于點E,F,AE和BF交于點P.如圖,點點同學發現當射線AM,BN交于點C;且∠ACB=60°時,有以下兩個結論:
①∠APB=120°;②AF+BE=AB.
那么,當AM∥BN時:
(1)點點發現的結論還成立嗎?若成立,請給予證明;若不成立,請求出∠APB的度數,寫出AF,BE,AB長度之間的等量關系,并給予證明;
(2)設點Q為線段AE上一點,QB=5,若AF+BE=16,四邊形ABEF的面積為32![]() ,求AQ的長.
,求AQ的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一般情況下![]() 不成立,但有些數可以使得它成立,例如:
不成立,但有些數可以使得它成立,例如: ![]() .我們稱使得
.我們稱使得![]() 成立的一對數
成立的一對數![]() ,
, ![]() 為“相伴數對”,記為
為“相伴數對”,記為![]() .
.
(1)若![]() 是“相伴數對”,求
是“相伴數對”,求![]() 的值;
的值;
(2)寫出一個“相伴數對” ![]() ,其中
,其中![]() 且
且![]() ;
;
(3)若![]() 是“相伴數對”,求代數式
是“相伴數對”,求代數式![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF//BC交AC于M,若CM=5,則CE2+CF2等于( )

A. 100 B. 75 C. 120 D. 125
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com