
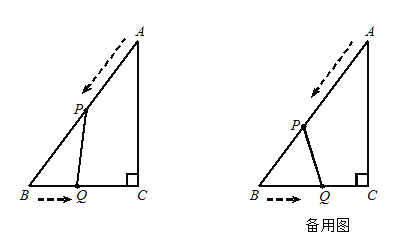
【題目】如圖12,在△ABC中,∠C=90°,AB=10cm,BC=6cm. 點P從點A出發,沿AB邊以2 cm/s的速度向點B勻速移動;點Q從點B出發,沿BC邊以1 cm/s的速度向點C勻速移動. 當一個運動點到達終點時,另一個運動點也隨之停止運動,設運動的時間為t(s).
(1)當PQ∥AC時,求t的值;
(2)當t為何值時,QB=QP;
(3)當t為何值時,△PBQ的面積等于4.8cm 2.
【答案】(1)t=![]() (2)t=
(2)t=![]() (3)當t為2s或3s時,△PBQ的面積等于4.8cm 2
(3)當t為2s或3s時,△PBQ的面積等于4.8cm 2
【解析】試題分析: ![]()
![]() ,則
,則![]() 對應邊成比例
對應邊成比例![]() ,即可求出
,即可求出![]() 的值.
的值.
![]() 當
當![]() 時,過點
時,過點![]() 作
作![]() 于
于![]() ,由
,由![]() 可以推出
可以推出![]() 對應邊成比例,則
對應邊成比例,則![]() ,即可求出
,即可求出![]() 的值.
的值.
![]() 過點
過點![]() 作
作![]() 于
于![]() ,則
,則![]() 則
則![]() 可以用
可以用![]() 表示出
表示出![]() ,根據三角形的面積公式,列出方程,解方程即可.
,根據三角形的面積公式,列出方程,解方程即可.
試題解析:
(1)![]() ,
,
![]()
∴![]() ,
,
即 ![]() ,
,
解得 t=![]() .
.
(2)解法1:
當![]() 時,過點
時,過點![]() 作
作![]() 于
于![]() (如圖4),則
(如圖4),則![]()
![]()
![]()
∴![]() ,
,
即![]()
解得 t=![]() .
.
解法2:
當![]() 時,過點
時,過點![]() 作
作![]() 于
于![]() (如圖4),則
(如圖4),則![]()
∵ 在![]() 中,cosB=
中,cosB=![]() ,
,
∴ 在![]() 中,
中,
cosB=![]() ,即
,即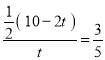 , 解得t=
, 解得t=![]() .
.
(![]() 中,
中, ![]() .
.
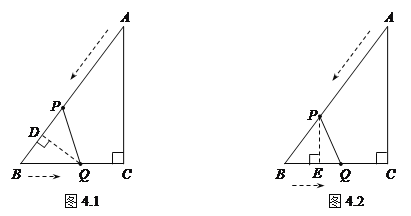
過點![]() 作
作![]() 于
于![]() ,則
,則![]() (如圖4.2).
(如圖4.2).
∵![]() .
.
![]()
∴![]() ,即
,即 ![]() , 解得
, 解得![]()
∴![]() 即
即![]()
整理得: ![]() 解這個方程,得
解這個方程,得![]()
![]()
∴ 當![]() 為2s或3s時,
為2s或3s時, ![]() 的面積等于4.8cm 2.
的面積等于4.8cm 2.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】閱讀材料,請回答下列問題.
材料一:我國古代數學家秦九韶在《數書九章》中記述了“三斜求積術”,即已知三角形的三邊長,求它的面積,用現代式子表示即為: ①(其中
①(其中![]() 為三角形的三邊長,
為三角形的三邊長,![]() 為面積),而另一個文明古國古希臘也有求三角形面積的“海倫公式”;
為面積),而另一個文明古國古希臘也有求三角形面積的“海倫公式”;![]() ……②(其中
……②(其中![]() )
)
材料二:對于平方差公式:![]() 公式逆用可得:
公式逆用可得:![]() ,例:
,例:![]()
(1)若已知三角形的三邊長分別為4,5,7,請分別運用公式①和公式②,計算該三角形的面積;
(2)你能否由公式①推導出公式②?請試試,寫出推導過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() 上部分點坐標如表所示,下列說法錯誤的是( )
上部分點坐標如表所示,下列說法錯誤的是( )
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -6 | 0 | 4 | 6 | 6 | … |
A. 拋物線與y軸的交點為(0,6) B. 拋物線的對稱軸是在y軸的右側;
C. 拋物線一定經過點(3,0) D. 在對稱軸左側,y隨x增大而減小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們定義:
在一個三角形中,如果一個角的度數是另一個角的度數![]() 倍,那么這樣的三角形我們稱之為“和諧三角形”.如:三個內角分別為
倍,那么這樣的三角形我們稱之為“和諧三角形”.如:三個內角分別為![]() ,
,![]() ,
,![]() 的三角形是“和諧三角形”
的三角形是“和諧三角形”
概念理解:
如圖,![]() ,在射線
,在射線![]() 上找一點
上找一點![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,以
,以![]() 為端點作射線
為端點作射線![]() ,交線段
,交線段![]() 于點
于點![]() (點
(點![]() 不與
不與![]() 重合)
重合)

(1)![]() 的度數為 ,
的度數為 ,![]() (填“是”或“不是”)“和諧三角形”
(填“是”或“不是”)“和諧三角形”
(2)若![]() ,求證:
,求證:![]() 是“和諧三角形”.
是“和諧三角形”.
應用拓展:
如圖,點![]() 在
在![]() 的邊
的邊![]() 上,連接
上,連接![]() ,作
,作![]() 的平分線
的平分線![]() 交于點
交于點![]() ,在
,在![]() 上取點
上取點![]() ,使
,使![]() ,
,![]() .若
.若![]() 是“和諧三角形”,求
是“和諧三角形”,求![]() 的度數.
的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c與x軸交于A、B兩點,與y軸交于點C, D為OC的中點,直線AD交拋物線于點E(2,6),且△ABE與△ABC的面積之比為3∶2.

(1)求這條拋物線對應的函數關系式;
(2)連結BD,試判斷BD與AD的位置關系,并說明理由;
(3)連結BC交直線AD于點M,在直線AD上,是否存在這樣的點N(不與點M重合),使得以A、B、N為頂點的三角形與△ABM相似?若存在,請求出點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為美化校園,準備在長35米,寬20米的長方形場地上,修建若干條寬度相同的道路,余下部分作草坪,并請全校學生參與方案設計,現有3位同學各設計了一種方案,圖紙分別如圖l、圖2和圖3所示(陰影部分為草坪).

請你根據這一問題,在每種方案中都只列出方程不解.
①甲方案設計圖紙為圖l,設計草坪的總面積為600平方米.
②乙方案設計圖紙為圖2,設計草坪的總面積為600平方米.
③丙方案設計圖紙為圖3,設計草坪的總面積為540平方米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一個單位面積為1的方格紙上,△A1A2A3,△A3A4A5,△A5A6A7,……是斜邊在x軸上,且斜邊長分別為2,4,6,……的等腰直角三角形.若△A1A2A3的頂點坐標分別為A1(2,0),A2(1,-1),A3(0,0),則依圖中所示規律,點A2019的橫坐標為( )
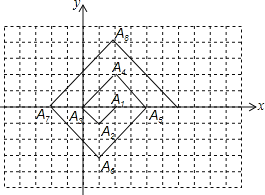
A. 1010B. ![]() C. 1008D.
C. 1008D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠1=∠2,DE⊥BC,AB⊥BC,試說明:∠A=∠3.

解:因為DE⊥BC,AB⊥BC(已知),
所以∠DEC=∠ABC=90°(____________),
所以DE∥AB(____________________),
所以∠2=________(____________________),
∠1=________(____________________).
因為∠1=∠2(已知),
所以∠A=∠3(等量代換).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com