
【題目】如圖,在□ABCD中,點E、F分別在邊AB、DC上,下列條件不能使四邊形EBFD是平行四邊形的條件是( )

A.DE=BFB.AE=CFC.DE∥FBD.∠ADE=∠CBF
【答案】A
【解析】
根據平行四邊形的性質可得AB∥CD,添加DE=BF后,滿足一組對邊平行,另一組對邊相等,不符合平行四邊形的判定方法,進而可判斷A項;
根據平行四邊形的性質可得AB∥CD,AB=CD,進一步即得BE=DF,根據一組對邊平行且相等的四邊形是平行四邊形即可判斷B項;
根據平行四邊形的性質可得AB∥CD,進而根據平行四邊形的定義可判斷C項;
根據平行四邊形的性質可證明△ADE≌△CBF,進而可得AE=CF,DE=BF,然后根據兩組對邊相等的四邊形是平行四邊形即可判斷D項.
解:A、∵四邊形ABCD是平行四邊形,∴AB∥CD,由DE=BF,不能判定四邊形EBFD是平行四邊形,所以本選項符合題意;
B、∵四邊形ABCD是平行四邊形,∴AB∥CD,AB=CD,
∵AE=CF,∴BE=DF,∴四邊形EBFD是平行四邊形,所以本選項不符合題意;
C、∵四邊形ABCD是平行四邊形,∴AB∥CD,
∵DE∥FB,∴四邊形EBFD是平行四邊形,所以本選項不符合題意;
D、∵四邊形ABCD是平行四邊形,∴∠A=∠C,AD=CB,AB=CD,
∵∠ADE=∠CBF,∴△ADE≌△CBF(ASA),∴AE=CF,DE=BF,
∴BE=DF,∴四邊形EBFD是平行四邊形,所以本選項不符合題意.
故選:A.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線y=﹣x+2與反比例函數y=![]() (k≠0)的圖象交于A(a,3),B(3,b)兩點,過點A作AC⊥x軸于點C,過點B作BD⊥x軸于點D.
(k≠0)的圖象交于A(a,3),B(3,b)兩點,過點A作AC⊥x軸于點C,過點B作BD⊥x軸于點D.
(1)求a,b的值及反比例函數的解析式;
(2)若點P在直線y=﹣x+2上,且S△ACP=S△BDP,請求出此時點P的坐標;
(3)在x軸正半軸上是否存在點M,使得△MAB為等腰三角形?若存在,請直接寫出M點的坐標;若不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD和四邊形ACED都是平行四邊形,點R為DE的中點,BR分別交AC和CD于點P,Q.
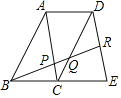
(1)求證:△ABP∽△DQR;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“足球運球”是中考體育必考項目之一.蘭州市某學校為了解今年九年級學生足球運球的掌握情況,隨機抽取部分九年級學生足球運球的測試成績作為一個樣本,按A,B,C,D四個等級進行統計,制成了如下不完整的統計圖.(說明:A級:8分﹣10分,B級:7分﹣7.9分,C級:6分﹣6.9分,D級:1分﹣5.9分)
根據所給信息,解答以下問題:
(1)在扇形統計圖中,C對應的扇形的圓心角是 度;
(2)補全條形統計圖;
(3)所抽取學生的足球運球測試成績的中位數會落在 等級;
(4)該校九年級有300名學生,請估計足球運球測試成績達到A級的學生有多少人?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計劃建一個長方形養雞場,為了節省材料,利用一道足夠長的墻做為養雞場的一邊,另三邊用鐵絲網圍成,如果鐵絲網的長為35m.
(1)計劃建養雞場面積為150m2,則養雞場的長和寬各為多少?
(2)能否建成的養雞場面積為160m2?如果能,請算出養雞場的長和寬;如果不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為滿足市場需求,某超市在五月初五“端午節”來臨前夕,購進一種品牌
粽子,每盒進價是40元,超市規定每盒售價不得少于45元.根據以往銷售經驗發現:當售價定為每盒45元時,每天可賣出700盒,每盒售價每提高1元,每天要少賣出20盒.
(1)試求出每天的銷售量y(盒)與每盒售價![]() (元)之間的函數關系式;(4分)
(元)之間的函數關系式;(4分)
(2)當每盒售價定為多少元時,每天銷售的利潤![]() (元)最大?最大利潤是多少?(6分)
(元)最大?最大利潤是多少?(6分)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com