
【題目】如圖,已知Rt△ABC中,∠ACB=90°,以斜邊AB為邊向外作正方形ABDE,且正方形的對角線交于點O,連結OC.已知AC=5,OC=6 ![]() ,則另一直角邊BC的長為 .
,則另一直角邊BC的長為 . 
【答案】4
【解析】過O作OF垂直于BC,再過A作AM垂直于OF,由四邊形ABDE為正方形,得到OA=OB,∠AOB為直角,可得出兩個角互余,再由AM垂直于MO,得到△AOM為直角三角形,其兩個銳角互余,利用同角的余角相等可得出一對角相等,再由一對直角相等,OA=OB,利用AAS可得出△AOM與△BOF全等,由全等三角形的對應邊相等可得出AM=OF,OM=FB,由三個角為直角的四邊形為矩形得到ACFM為矩形,根據矩形的對邊相等可得出AC=MF,AM=CF,等量代換可得出CF=OF,即△COF為等腰直角三角形,由斜邊OC的長,利用勾股定理求出OF與CF的長,根據OF﹣MF求出OM的長,即為FB的長,由CF+FB即可求出BC的長.解法一:如圖1所示,過O作OF⊥BC,過A作AM⊥OF,∵四邊形ABDE為正方形,∴∠AOB=90°,OA=OB,∴∠AOM+∠BOF=90°,又∠AMO=90°,∴∠AOM+∠OAM=90°,∴∠BOF=∠OAM,在△AOM和△BOF中, 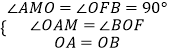 ,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四邊形ACFM為矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF為等腰直角三角形,∵OC=6
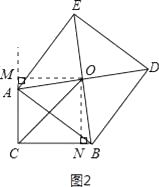
,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四邊形ACFM為矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF為等腰直角三角形,∵OC=6 ![]() ,∴根據勾股定理得:CF2+OF2=OC2 , 解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,則BC=CF+BF=6+1=7.故答案為:7.解法二:如圖2所示,過點O作OM⊥CA,交CA的延長線于點M;過點O作ON⊥BC于點N.易證△OMA≌△ONB,∴OM=ON,MA=NB.∴O點在∠ACB的平分線上,∴△OCM為等腰直角三角形.∵OC=6
,∴根據勾股定理得:CF2+OF2=OC2 , 解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,則BC=CF+BF=6+1=7.故答案為:7.解法二:如圖2所示,過點O作OM⊥CA,交CA的延長線于點M;過點O作ON⊥BC于點N.易證△OMA≌△ONB,∴OM=ON,MA=NB.∴O點在∠ACB的平分線上,∴△OCM為等腰直角三角形.∵OC=6 ![]() ,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案為:7.
,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案為:7.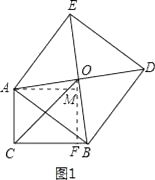


科目:初中數學 來源: 題型:
【題目】任意拋擲一枚骰子兩次,骰子停止轉動后,計算朝上的點數的和.
(1)和最小的是多少,和最大的是多少?
(2)下列事件:①點數的和為7;②點數的和為1;③點數的和為15.哪些是不可能性事件?哪些是不確定事件?
(3)點數的和為7與點數的和為2的可能性誰大?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC是不規則三角形,若線段AD把△ABC分為面積相等的兩部分,則線段AD應該是( )
A.三角形的角平分線
B.三角形的中線
C.三角形的高
D.以上都不對
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于函數y=2x,下列結論中正確的是( )
A. 函數圖象都經過點(2,1) B. 函數圖象都經過第二、四象限
C. y隨x的增大而增大 D. 不論x取何值,總有y>0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某企業決定用![]() 萬元援助災區
萬元援助災區![]() 所學校,用于搭建帳篷和添置教學設備。根據各校不同的受災情況,該企業捐款的分配方案如下:所有學校得到的捐款數都相等,到第
所學校,用于搭建帳篷和添置教學設備。根據各校不同的受災情況,該企業捐款的分配方案如下:所有學校得到的捐款數都相等,到第![]() 所學校的捐款恰好分完,捐款的分配方法如下表所示. (其中
所學校的捐款恰好分完,捐款的分配方法如下表所示. (其中![]() ,
,![]() ,
,![]() 都是正整數)
都是正整數)
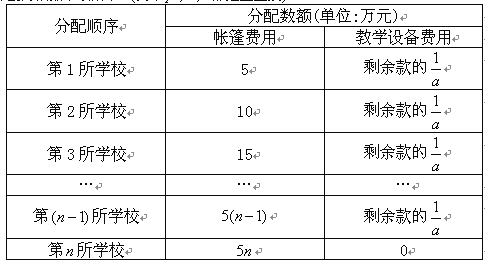
根據以上信息,解答下列問題:
(1)寫出![]() 與
與![]() 的關系式;
的關系式;
(2)當![]() 時,該企業能援助多少所學校?
時,該企業能援助多少所學校?
(3)根據震區災情,該企業計劃再次提供不超過![]() 萬元的捐款,按照原來的分配方案援助其它學校.若
萬元的捐款,按照原來的分配方案援助其它學校.若![]() 由 (2)確定,則再次提供的捐款最多又可以援助多少所學校?
由 (2)確定,則再次提供的捐款最多又可以援助多少所學校?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下面推理過程.在括號內的橫線上填空或填上推理依據.
如圖,已知:AB∥EF,EP⊥EQ,∠EQC+∠APE=90°,求證:AB∥CD
證明:∵AB∥EF
∴∠APE=()
∵EP⊥EQ
∴∠PEQ=()
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
∵∠EQC+∠APE=90°
∴∠EQC=
∴EF∥()
∴AB∥CD()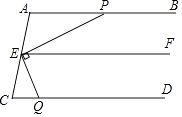
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB=4cm,BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,則四邊形ABCD的面積為( ) 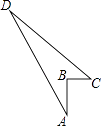
A.6cm2
B.30cm2
C.24cm2
D.36cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是平行四邊形,以AB為直徑的⊙O經過點D,E是⊙O上一點,且∠AED=45.
(1)試判斷CD與⊙O的位置關系,并證明你的結論;
(2)若⊙O的半徑為3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
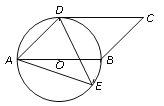
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com