
【題目】為了解某小區(qū)小孩暑期的學(xué)習(xí)情況,王老師隨機(jī)調(diào)查了該小區(qū)8個(gè)小孩某天的學(xué)習(xí)時(shí)間,結(jié)果如下(單位:小時(shí)):1.5,1.5,3,4,2,5,2.5,4.5,關(guān)于這組數(shù)據(jù),下列結(jié)論錯(cuò)誤的是( )
A. 極差是3.5 B. 眾數(shù)是1.5 C. 中位數(shù)是3 D. 平均數(shù)是3
 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(問題背景)
如圖,在平面直角坐標(biāo)系![]() 中,點(diǎn)
中,點(diǎn)![]() 的坐標(biāo)是
的坐標(biāo)是![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 軸上的一個(gè)動點(diǎn).當(dāng)點(diǎn)
軸上的一個(gè)動點(diǎn).當(dāng)點(diǎn)![]() 在
在![]() 軸上移動時(shí),始終保持
軸上移動時(shí),始終保持![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() (點(diǎn)
(點(diǎn)![]() 、
、![]() 、
、![]() 按逆時(shí)針方向排列);當(dāng)點(diǎn)
按逆時(shí)針方向排列);當(dāng)點(diǎn)![]() 移動到點(diǎn)
移動到點(diǎn)![]() 時(shí),得到等腰直角三角形
時(shí),得到等腰直角三角形![]() (此時(shí)點(diǎn)
(此時(shí)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合).
重合).
(初步探究)
(1)寫出點(diǎn)![]() 的坐標(biāo)______.
的坐標(biāo)______.
(2)點(diǎn)![]() 在
在![]() 軸上移動過程中,當(dāng)?shù)妊苯侨切?/span>
軸上移動過程中,當(dāng)?shù)妊苯侨切?/span>![]() 的頂點(diǎn)
的頂點(diǎn)![]() 在第四象限時(shí),連接
在第四象限時(shí),連接![]() .
.
求證:![]() ;
;
(深入探究)
(3)當(dāng)點(diǎn)![]() 在
在![]() 軸上移動時(shí),點(diǎn)
軸上移動時(shí),點(diǎn)![]() 也隨之運(yùn)動.經(jīng)過探究發(fā)現(xiàn),點(diǎn)
也隨之運(yùn)動.經(jīng)過探究發(fā)現(xiàn),點(diǎn)![]() 的橫坐標(biāo)總保持不變,請直接寫出點(diǎn)
的橫坐標(biāo)總保持不變,請直接寫出點(diǎn)![]() 的橫坐標(biāo):______.
的橫坐標(biāo):______.
(拓展延伸)
(4)點(diǎn)![]() 在
在![]() 軸上移動過程中,當(dāng)
軸上移動過程中,當(dāng)![]() 為等腰三角形時(shí),直接寫出此時(shí)點(diǎn)
為等腰三角形時(shí),直接寫出此時(shí)點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
 備用圖
備用圖
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】對于平面直角坐標(biāo)系中的任意兩點(diǎn)![]() ,
,![]() ,我們把
,我們把![]() 叫
叫![]() ,
,![]() 兩點(diǎn)間的“平面距離”,記作
兩點(diǎn)間的“平面距離”,記作![]() .
.
(![]() )已知
)已知![]() 為坐標(biāo)原點(diǎn),動點(diǎn)
為坐標(biāo)原點(diǎn),動點(diǎn)![]() 是坐標(biāo)軸上的點(diǎn),滿足
是坐標(biāo)軸上的點(diǎn),滿足![]() ,請寫出點(diǎn)
,請寫出點(diǎn)![]() 的坐標(biāo).答:__________.
的坐標(biāo).答:__________.
(![]() )設(shè)
)設(shè)![]() 是平面上一點(diǎn),
是平面上一點(diǎn),![]() 是直線
是直線![]() 上的動點(diǎn),我們定義
上的動點(diǎn),我們定義![]() 的最小值叫做
的最小值叫做![]() 到直線
到直線![]() 的“平面距離”.試求點(diǎn)
的“平面距離”.試求點(diǎn)![]() 到直線
到直線![]() 的“平面距離”.
的“平面距離”.
(![]() )在上面的定義基礎(chǔ)上,我們可以定義平面上一條直線
)在上面的定義基礎(chǔ)上,我們可以定義平面上一條直線![]() 與⊙
與⊙![]() 的“直角距離”:在直線
的“直角距離”:在直線![]() 與⊙
與⊙![]() 上各自任取一點(diǎn),此兩點(diǎn)之間的“平面距離”的最小值稱為直線
上各自任取一點(diǎn),此兩點(diǎn)之間的“平面距離”的最小值稱為直線![]() 與⊙
與⊙![]() 的“平面距離”,記作
的“平面距離”,記作![]() .
.
試求直線![]() 與圓心在直線坐標(biāo)系原點(diǎn)、半徑是
與圓心在直線坐標(biāo)系原點(diǎn)、半徑是![]() 的⊙
的⊙![]() 的直角距離
的直角距離![]() __________.(直接寫出答案)
__________.(直接寫出答案)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】請閱讀下列材料:
問題:如圖,在正方形![]() 和平行四邊形
和平行四邊形![]() 中,點(diǎn)
中,點(diǎn)![]() ,
,![]() ,
,![]() 在同一條直線上,
在同一條直線上,![]() 是線段
是線段![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() ,
,![]() .
.
探究:當(dāng)![]() 與
與![]() 的夾角為多少度時(shí),平行四邊形
的夾角為多少度時(shí),平行四邊形![]() 是正方形?
是正方形?
小聰同學(xué)的思路是:首先可以說明四邊形![]() 是矩形;然后延長
是矩形;然后延長![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,構(gòu)造全等三角形,經(jīng)過推理可以探索出問題的答案.
,構(gòu)造全等三角形,經(jīng)過推理可以探索出問題的答案.
請你參考小聰同學(xué)的思路,探究并解決這個(gè)問題.

(1)求證:四邊形![]() 是矩形;
是矩形;
(2)![]() 與
與![]() 的夾角為________度時(shí),四邊形
的夾角為________度時(shí),四邊形![]() 是正方形.
是正方形.
理由:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知一元二次方程(a+1)x2﹣ax+a2﹣a﹣2=0的一個(gè)根與方程(a+1)x2+ax﹣a2+a+2=0的一個(gè)根互為相反數(shù),那么(a+1)x2+ax﹣a2+a+2=0的根是( )
A. 0,﹣![]() B. 0,
B. 0,![]() C. ﹣1,2 D. 1,﹣2
C. ﹣1,2 D. 1,﹣2
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校為美化校園,計(jì)劃對面積為1800m2的區(qū)域進(jìn)行綠化,安排甲、乙兩個(gè)工程隊(duì)完成.已知甲隊(duì)每天能完成綠化的面積是乙隊(duì)每天能完成綠化的面積的2倍,并且在獨(dú)立完成面積為400 m2區(qū)域的綠化時(shí),甲隊(duì)比乙隊(duì)少用4天.
(1)求甲、乙兩工程隊(duì)每天能完成綠化的面積分別是多少m2?
(2)若學(xué)校每天需付給甲隊(duì)的綠化費(fèi)用是0.4萬元,乙隊(duì)為0.25萬元,要使這次的綠化總費(fèi)用不超過8萬元,至少應(yīng)安排甲隊(duì)工作多少天?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙、丙三位運(yùn)動員在相同條件下各射靶![]() 次,每次射靶的成績?nèi)缦拢?/span>
次,每次射靶的成績?nèi)缦拢?/span>
甲:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
丙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)根據(jù)以上數(shù)據(jù)完成下表:
平均數(shù) | 中位數(shù) | 方差 | |
甲 |
|
| __________ |
乙 | __________ |
|
|
丙 |
| __________ |
|
(2)根據(jù)表中數(shù)據(jù)分析,哪位運(yùn)動員的成績最穩(wěn)定.并簡要說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
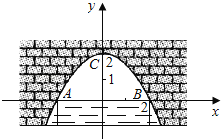
【題目】圖中是拋物線形拱橋,當(dāng)拱頂離水面2m時(shí),水面寬4m,建立如圖所示的平面直角坐標(biāo)系:
(1)求拱橋所在拋物線的解析式;
(2)當(dāng)水面下降1m時(shí),則水面的寬度為多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,直線l1:y=﹣![]() x與反比例函數(shù)y=
x與反比例函數(shù)y=![]() 的圖象交于A,B兩點(diǎn)(點(diǎn)A在點(diǎn)B左側(cè)),已知A點(diǎn)的縱坐標(biāo)是2:
的圖象交于A,B兩點(diǎn)(點(diǎn)A在點(diǎn)B左側(cè)),已知A點(diǎn)的縱坐標(biāo)是2:
(1)求反比例函數(shù)的表達(dá)式;
(2)將直線l1:y=﹣![]() x向上平移后的直線l2與反比例函數(shù)y=
x向上平移后的直線l2與反比例函數(shù)y=![]() 在第二象限內(nèi)交于點(diǎn)C,如果△ABC的面積為30,求平移后的直線l2的函數(shù)表達(dá)式.
在第二象限內(nèi)交于點(diǎn)C,如果△ABC的面積為30,求平移后的直線l2的函數(shù)表達(dá)式.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com