Question

已知關于x的方程（a²-1）x²-（a+1）x+1=0的兩實根互為倒數，求a的值．

Answer 1

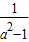
【答案】分析：可設x₁、x₂為所給方程的兩根，兩實根互為倒數，即x₁•x₂==1，可以求出a的值．同時注意舍去不合題意的a值．
解答：解：設x₁、x₂為所給方程的兩根，
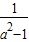
由x₁•x₂==1 （3分）
得a²-1=1，a²=2，
∴a=±
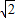
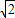
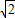
當a=時，方程為x²-（+1）x+1=0，
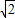
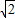
△=（+1）²-4=2-1＞0，方程有兩實根；（6分）
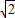
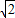
當a=-時，方程為x²-（-1）x+1=0，
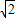
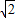
△=（-1）²-4=-2-1＜0，方程無實根．
故應舍去a=-．
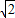
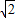
∴a=．（8分）
點評：本題通過兩實根互為倒數重點考查了一元二次方程根的判別式和根與系數的關系，是一個綜合性的題目，也是一個難度中等的題目．