
【題目】如圖,兩塊直角三角板的直角頂點O重合在一起,若∠BOC=![]() ∠AOD,則∠BOC的度數為( )
∠AOD,則∠BOC的度數為( )
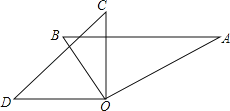
A.22.5°B.30°C.45°D.60°
 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案科目:初中數學 來源: 題型:
【題目】為了了解某校七年級800名學生的跳繩情況(60秒跳繩的次數),隨機對該年級50名學生進行了調查,根據收集的數據繪制了如圖所示的頻數分布直方圖(每組數據包括左端值不包括右端值,如最左邊第一組的次數x為:![]() ,則以下說法正確的是( )
,則以下說法正確的是( )
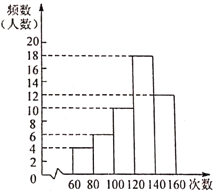
A. 跳繩次數最多的是160次
B. 大多數學生跳繩次數在140-160范圍內
C. 跳繩次數不少于100次的占80%
D. 由樣本可以估計全年級800人中跳繩次數在60-80次的大約有70人
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近幾年,全社會對空氣污染問題越來越重視,空氣凈化器的銷量也在逐年增加.某商場從廠家購進了A、B兩種型號的空氣凈化器,兩種凈化器的銷售相關信息見下表:
A型銷售數量(臺) | B型銷售數量(臺) | 總利潤(元) |
5 | 10 | 2000 |
10 | 5 | 2500 |
(1)每臺A型空氣凈化器和B型空氣凈化器的銷售利潤分別是多少?
(2)該公司計劃一次購進兩種型號的空氣凈化器共100臺,其中B型空氣凈化器的進貨量不少于A型空氣凈化器的2倍,為使該公司銷售完這100臺空氣凈化器后的總利潤最大,請你設計相應的進貨方案;
(3)已知A型空氣凈化器的凈化能力為300m3/小時,B型空氣凈化器的凈化能力為200m3/小時,某長方體室內活動場地的總面積為200m2 , 室內墻高3m,該場地負責人計劃購買5臺空氣凈化器每天花費30分鐘將室內就歐諾個氣凈化一新,若不考慮空氣對流等因素,至少要購買A型空氣凈化器多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解龍崗區學生喜歡球類活動的情況,采取抽樣調查的方法,從足球、乒乓球、籃球、排球等四個方面調查了全班學生的興趣愛好,根據調查的結果繪制成如圖所示的兩幅不完整的統計圖(如圖①,②,要求每位學生只能選擇一種自己喜歡的球類),請你根據圖中提供的信息解答下列問題:
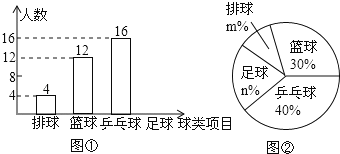
(1)本次共調查的學生人數為___,并把條形統計圖補充完整;
(2)扇形統計圖中m=___,n=___;
(3)表示“足球”的扇形的圓心角是___度;
(4)若龍崗區初中學生共有60000人,則喜歡乒乓球的有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
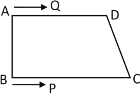
【題目】如圖,在四邊形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,點Q從點A出發以1 cm/s的速度向點D運動,點P從點B出發以2 cm/s的速度向點C運動,P,Q兩點同時出發,當點P到達點C時,兩點同時停止運動.若設運動時間為t(s)
(1)直接寫出:QD=______cm,PC=_______cm;(用含t的式子表示)
(2)當t為何值時,四邊形PQDC為平行四邊形?
(3)若點P與點C不重合,且DQ≠DP,當t為何值時,△DPQ是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,AC=BC,P是△ABC內的一點,PA=3,PB=1,CD=PC=2,CD⊥PC.
(1)找出圖中一對全等三角形,并證明;
(2)求∠BPC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
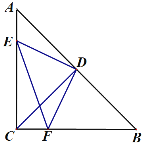
【題目】如圖在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于點D,點E、F分別在AC、BC上,且∠EDF=90°.
(1)求證:△AED≌△CFD;
(2)試判斷CE、CF與CD之間的數量關系,并說明理由;
(3)若CF=1,CE=3,試求DF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校數學興趣小組成員小華對本班上學期期末考試數學成績(成績取整數,滿分為100分)作了統計分析,繪制成如下頻數分布直方圖和頻數、頻率分布表.請你根據圖表提供的信息,解答下列問題:
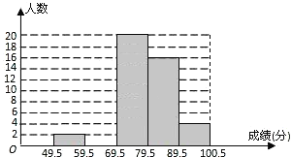
分組 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合計 |
頻數 | 2 |
| 20 | 16 | 4 | 50 |
頻率 | 0.04 | 0.16 | 0.40 | 0.32 |
| 1 |
(1)頻數、頻率分布表中![]() ,
,![]() ;
;
(2)補全頻數分布直方圖;
(3)數學老師準備從不低于90分的學生中選1人介紹學習經驗,那么取得了93分的小華被選上的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com