
【題目】某商店以每件50元的價格購進800件![]() 恤,第一個月以單價80元銷售,售出了200件.第二個月如果單價不變,預計仍可售出200件,該商店為增加銷售量決定降價銷售,根據市場調查,單價每降低1元,可多銷售出10件,但最低單價應不低于50元,第二個月結束后,該商店對剩余的T恤一次性清倉,清倉時單價為40元.設第二個月單價降低
恤,第一個月以單價80元銷售,售出了200件.第二個月如果單價不變,預計仍可售出200件,該商店為增加銷售量決定降價銷售,根據市場調查,單價每降低1元,可多銷售出10件,但最低單價應不低于50元,第二個月結束后,該商店對剩余的T恤一次性清倉,清倉時單價為40元.設第二個月單價降低![]() 元,
元,
(1)填表(用含![]() 的代數式完成表格中的①②③處)
的代數式完成表格中的①②③處)
時間 | 第一個月 | 第二個月 | 清倉 |
單價(元) | 80 | _______ | 40 |
銷售量(件) | 200 | _______ | _______ |
(2)如果該商店希望通過銷售這800件![]() 恤獲利9000元,那么第二個月單價降低多少元?
恤獲利9000元,那么第二個月單價降低多少元?
【答案】(1)80-x,200+10x,400-10x.(2)10元.
【解析】
(1)第二個月的單價=第一個月的單價-降低的價格,銷售量=200+10×降低的單價;清倉時的銷售量為:800-第一個月的銷售量-第二個月的銷售量;
(2)等量關系為:總售價-總進價=9000.把相關數值代入計算即可.
解:(1)填表:
時間 | 第一周 | 第二周 | 清倉時 |
單價(元) | 80 | 80-x | 40 |
銷售量(件) | 200 | 200+10x | 400-10x |
故答案為80-x,200+10x,400-10x.
(2)80×200+(80-x)(200+10x)+40×[800-200-(200+10x)]-800×50=9000,
x2-20x+100=0,
解得:x1=x2=10,
當x=10時,80-x=70.80-70=10(元)
答:第二個月的單價應降低10元.


科目:初中數學 來源: 題型:
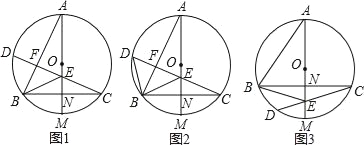
【題目】已知AM是⊙O直徑,弦BC⊥AM,垂足為點N,弦CD交AM于點E,連按AB和BE.
(1)如圖1,若CD⊥AB,垂足為點F,求證:∠BED=2∠BAM;
(2)如圖2,在(1)的條件下,連接BD,若∠ABE=∠BDC,求證:AE=2CN;
(3)如圖3,AB=CD,BE:CD=4:7,AE=11,求EM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
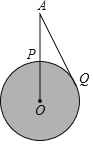
【題目】如圖,某航天飛機在地球表面點P的正上方A處,從A處觀測到地球上的最遠點Q,即AQ是⊙O的切線,若∠QAP=α,地球半徑為R,
求:(1)航天飛機距地球表面的最近距離AP的長;
(2)P、Q兩點間的地面距離,即![]() 的長.(注:本題最后結果均用含α,R的代數式表示)
的長.(注:本題最后結果均用含α,R的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,已知
,已知![]() ,
,![]()
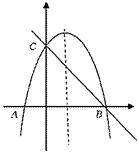
(1)求該拋物線和直線![]() 的函數表達式;
的函數表達式;
(2)點![]() 是拋物線上第一象限內的一個動點,當點
是拋物線上第一象限內的一個動點,當點![]() 運動到什么位置時,
運動到什么位置時,![]() 的面積
的面積![]() 最大?求
最大?求![]() 面積
面積![]() 的最大值及此時點
的最大值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
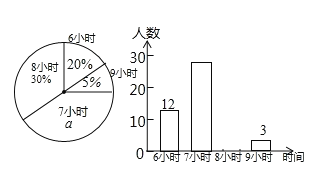
【題目】為了了解某校初中各年級學生每天的平均睡眠時間(單位:h,精確到1h),抽樣調查了部分學生,并用得到的數據繪制了下面兩幅不完整的統計圖.
請你根據圖中提供的信息,回答下列問題:
(1)求出扇形統計圖中百分數a的值為 ,所抽查的學生人數為 .
(2)求出平均睡眠時間為8小時的人數,并補全頻數直方圖.
(3)求出這部分學生的平均睡眠時間的眾數和平均數.
(4)如果該校共有學生1200名,請你估計睡眠不足(少于8小時)的學生數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一矩形OABC放在直角坐標系中,O為坐標原點,點A在y軸正半軸上,點E是邊AB上的一個動點![]() 不與點A、B重合
不與點A、B重合![]() ,過點E的反比例函數
,過點E的反比例函數![]() 的圖象與邊BC交于點F
的圖象與邊BC交于點F
![]() 若
若![]() 的面積為
的面積為![]() ,且
,且![]() ,求k的值;
,求k的值;
![]() 若
若![]() ,
,![]() ,反比例函數
,反比例函數![]() 的圖象與邊AB、邊BC交于點E和F,當
的圖象與邊AB、邊BC交于點E和F,當![]() 沿EF折疊,點B恰好落在OC上,求k的值.
沿EF折疊,點B恰好落在OC上,求k的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,函數![]() 和
和![]() 的圖象分別為直線
的圖象分別為直線![]() ,
,![]() ,過點(1,0)作
,過點(1,0)作![]() 軸的垂線交
軸的垂線交![]() 于點
于點![]() ,過
,過![]() 點作
點作![]() 軸的垂線交
軸的垂線交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 軸的垂線交
軸的垂線交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 軸的垂線交
軸的垂線交![]() 于點
于點![]() ,…依次進行下去,則點
,…依次進行下去,則點![]() 的坐標為_________.
的坐標為_________.

查看答案和解析>>
科目:初中數學 來源: 題型:
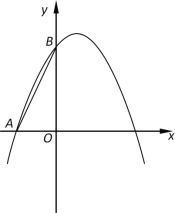
【題目】如圖,拋物線![]() 經過點A(﹣2,0),點B(0,4).
經過點A(﹣2,0),點B(0,4).
(1)求這條拋物線的表達式;
(2)P是拋物線對稱軸上的點,聯結AB、PB,如果∠PBO=∠BAO,求點P的坐標;
(3)將拋物線沿y軸向下平移m個單位,所得新拋物線與y軸交于點D,過點D作DE∥x軸交新拋物線于點E,射線EO交新拋物線于點F,如果EO=2OF,求m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com