
 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:初中數學 來源: 題型:
 (1)計算:(
(1)計算:(| 2 |
| 8 |
| x2-2xy+y2 |
| x2-xy |
| x |
| y |
| y |
| x |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 點A重合.將線段AP繞點A逆時針旋轉到AQ,使∠PAQ=∠BAC,連接BP,CQ
點A重合.將線段AP繞點A逆時針旋轉到AQ,使∠PAQ=∠BAC,連接BP,CQ查看答案和解析>>
科目:初中數學 來源: 題型:
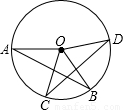
 (2012•密云縣一模)已知:如圖,在△ABC中,∠A=∠B=30°,D是AB 邊上一點,以AD為直徑作⊙O恰過點C.
(2012•密云縣一模)已知:如圖,在△ABC中,∠A=∠B=30°,D是AB 邊上一點,以AD為直徑作⊙O恰過點C.| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com