
【題目】如圖1,已知線段AB兩個端點坐標分別為A(a,0),B(0,b),且a,b滿足:![]()
(1)填空:a= ,b= .

(2)在坐標軸上是否存在點C,使S△ABC=6,若存在,求出點C的坐標,符不存在,說明理由;
(3)如圖2,若將線段Ba平移得到線段OD,其中B點對應O點,A點對應D點,點P(m,n)是線段OD上任意一點,請直接寫出m與n的關系式。
【答案】(1) -6,4;(2) C坐標為(-9,0),(-3,0),(0,2),(0,6);(3)2m=3n(-6≤m≤0).
【解析】
(1)根據非負數的性質列方程求解即可;
(2)根據點B的坐標,求出B到x軸的距離,再利用三角形的面積求出AC的長度,然后分點C在A點的左邊和右邊兩種情況討論求解;
(3)根據平移求出點D的坐標,然后求出OD的解析式,再把P點的坐標代入求解即可.
解:(1)∵![]()
∴a=-6,b=4,
故答案為-6,4;
(2)由(1)知,a=-6,b=4,
∴A(-6,0),B(0,4),
當點C在x軸上時,設C(c,0),
∴AC=|c+6|,
∵S△ABC=6,![]()
∴c=-9或c=-3,
∴C(-9,0)或(-3,0),
當點C在y軸上時,設C(0,c'),
∴BC=|c'-4|,
∵S△ABC=6,![]()
∴c'=2或c'=6,
∴C(0,2)或(0,6),
即:滿足條件的點C坐標為(-9,0),(-3,0),(0,2),(0,6);
(3)由(2)知,A(-6,0),B(0,4),
∵將線段BA平移得到線段OD,其中B點對應O點,A點對應D,
∴線段AB向下平移4個單位到線段OD,
∴D(-6,-4),設線段OD所在直線解析式為y=kx,
∴-6k=-4,


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2+bx+c(b,c為常數).
(1)當b=2,c=﹣3時,求二次函數圖象的頂點坐標;
(2)當c=10時,若在函數值y=1的情況下,只有一個自變量x的值與其對應,求此時二次函數的解析式;
(3)當c=b2時,若在自變量x的值滿足b≤x≤b+3的情況下,與其對應的函數值y的最小值為21,求此時二次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上三點M,O,N對應的數分別為-1,0,3,點P為數軸上任意一點,其對應的數為x.
![]()
(1)MN的長為 ;
(2)如果點P到點M、點N的距離相等,那么x的值是 ;
(3)數軸上是否存在點P,使點P到點M、點N的距離之和是8?若存在,直接寫出x的值;若不存在,請說明理由.
(4)如果點P以每分鐘1個單位長度的速度從點O向左運動,同時點M和點N分別以每分鐘2個單位長度和每分鐘3個單位長度的速度也向左運動.設t分鐘時點P到點M、點N的距離相等,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖A、B分別為數軸上的兩點,A點對應的數為-10,B點對應的數為90.
![]()
(1)請寫出與A,B兩點距離相等的M點對應的數;
(2)現在有一只電子螞蟻P從B點出發時,以3個單位/秒的速度向左運動,同時另一只電子螞蟻Q恰好從A點出發,以2個單位/秒的速度向右運動,設兩只電子螞蟻在數軸上的C點相遇,求C點對應的數是多少.
(3)若當電子螞蟻P從B點出發時,以3個單位/秒的速度向左運動,同時另一只電子螞蟻Q恰好從A點出發,以2個單位/秒的速度向右運動,求經過多長的時間兩只電子螞蟻在數軸上相距35個單位長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在“數學小論文”評比活動中,共征集到論文100篇,對論文評比的分數(分數為整數)整理后,分組畫出頻數分布直方圖(如圖),已知從左到右5個小長方形的高的比為l:3:7:6:3,那么在這次評比中被評為優秀的論文(分數大于或等于80分為優秀)有____篇.

查看答案和解析>>
科目:初中數學 來源: 題型:
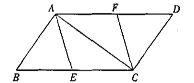
【題目】如圖,E、F分別是□ABCD的邊BC、AD上的點,且BE=DF
(1)求證:四邊形AECF是平行四邊形;
(2)若BC=10,∠BAC=90°,且四邊形AECF是菱形,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D、E、F分別在正三角形ABC的三邊上,且△DEF也是正三角形,若△ABC的邊長為a,△DEF的邊長為b.則△AEF的內切圓半徑為 . 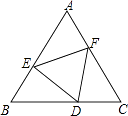
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著手機的普及,微信![]() 一種聊天軟件
一種聊天軟件![]() 的興起,許多人抓住這種機會,做起了“微商”,很多農產品也改變了原來的銷售模式,實行了網上銷售,這不剛大學畢業的小明把自家的冬棗產品也放到了網上,他原計劃每天賣100斤冬棗,但由于種種原因,實際每天的銷售量與計劃量相比有出入,下表是某周的銷售情況
的興起,許多人抓住這種機會,做起了“微商”,很多農產品也改變了原來的銷售模式,實行了網上銷售,這不剛大學畢業的小明把自家的冬棗產品也放到了網上,他原計劃每天賣100斤冬棗,但由于種種原因,實際每天的銷售量與計劃量相比有出入,下表是某周的銷售情況![]() 超額記為正,不足記為負
超額記為正,不足記為負![]() 單位:斤
單位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
與計劃量的差值 |
|
|
|
|
|
|
|
(1)根據記錄的數據可知前三天共賣出 ______ 斤;
(2)根據記錄的數據可知銷售量最多的一天比銷售量最少的一天多銷售 ______ 斤;
(3)本周實際銷售總量達到了計劃數量沒有?
(4)若冬季每斤按8元出售,每斤冬棗的運費平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,港口A在觀測站O的正東方向,OA=6km,某船從港口A出發,沿北偏東15°方向航行一段距離后到達B處,此時從觀測站O處測得該船位于北偏東60°的方向,則該船航行的距離(即AB的長)為 km.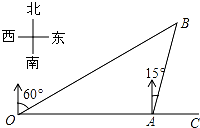
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com