
【題目】等邊△ABC的邊BC在射線BD上,動點P在等邊△ABC的BC邊上(點P與BC不重合),連接AP.
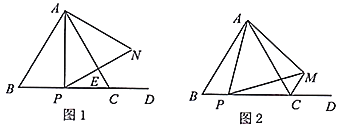
(1)如圖1,當點P是BC的中點時,過點P作![]() 于E,并延長PE至N點,使得
于E,并延長PE至N點,使得![]() .①若
.①若![]() ,試求出AP的長度;
,試求出AP的長度;
②連接CN,求證![]() .
.
(2)如圖2,若點M是△ABC的外角![]() 的角平分線上的一點,且
的角平分線上的一點,且![]() ,求證:
,求證:![]() .
.
【答案】(1)①AP![]() ;②證明見解析;(2)證明見解析.
;②證明見解析;(2)證明見解析.
【解析】
(1)①根據點P是BC的中點,利用等腰三角形三線合一的性質得AP⊥BC,再利用勾股定理即可求得答案;
②根據軸對稱的性質,證得∠NCE=∠PCE=![]() ,從而證得結論;
,從而證得結論;
(2)作∠CBF=60°,BF與MC的延長線相交于點F,連接PF,證明△BFC是等邊三角形,證得△ABP![]() △FBP,PM=PF,∠PMC=∠PFC,根據三角形外角的性質可得結論.
△FBP,PM=PF,∠PMC=∠PFC,根據三角形外角的性質可得結論.
(1)①在等邊△ABC中,
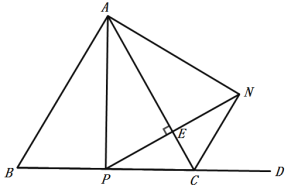
∵點P是BC的中點,![]() ,
,
∴AP⊥BC,![]() ,
,
∴AP=![]() ;
;
②∵![]() 且
且![]() ,
,
∴點N與點P關于直線AC對稱,
∴∠NCE=∠PCE=![]() ,
,
∴∠NCD=180![]() ∠NCE
∠NCE![]() ∠PCE=
∠PCE=![]() ,
,
∴∠NCD=∠B=![]() ,
,
∴![]() ;
;
(2)作∠CBF=60°,BF與MC的延長線相交于點F,連接PF,如圖:
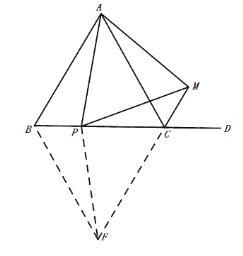
∵△ABC是等邊三角形,
∴∠ABC=∠ACB=60![]() ,
,
∴∠ACD=120![]() ,
,
∵CM平分∠ACD,
∴∠DCM=∠BCF=60![]() ,
,
∵∠CBF=60![]() ,
,
∴∠FBC=∠BCF=∠BFC=60![]() ,
,
∴△BFC是等邊三角形,
∵△ABC和△BFC都是等邊三角形,
∴AB=BC=BF,
在△ABP和△FBP中,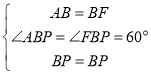 ,
,
∴△ABP![]() △FBP,
△FBP,
∴AP=PF,∠BAP=∠BFP,
∵AP=PM,
∴PM=PF,
∴∠PMC=∠PFC,
∵∠MCD=∠PMC +∠CPM=60![]() ,
,
∠BFC=∠BFP+∠PFC=60![]() ,
,
∴∠CPM=∠BFP =∠BAP,
∵∠APC=∠ABC+∠BAP=∠APM+∠CPM,
∴∠APM=60![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖:在平面直角坐標系中,已知![]() 的三個頂點的坐標分別為
的三個頂點的坐標分別為![]() ,
,![]() ,
,![]() .
.
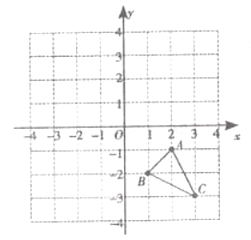
(1)將![]() 向上平移
向上平移![]() 個單位長度,再向左平移
個單位長度,再向左平移![]() 個單位長度,得到
個單位長度,得到![]() ,請畫出
,請畫出![]() (點
(點![]() ,
,![]() ,
,![]() 的對應點分別為
的對應點分別為![]() ,
,![]() ,
,![]() )
)
(2)請畫出與![]() 關于
關于![]() 軸對稱的
軸對稱的![]() (點
(點![]() ,
,![]() ,
,![]() 的對應點分別為
的對應點分別為![]() ,
,![]() ,
,![]() )
)
(3)請寫出![]() ,
,![]() 的坐標
的坐標
查看答案和解析>>
科目:初中數學 來源: 題型:
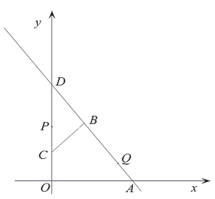
【題目】如圖,在平面直角坐標系中,已知點A的坐標為(15,0),點B的坐標為(6,12),點C的坐標為(0,6), 直線AB交y軸于點D, 動點P從點C出發沿著y軸正方向以每秒2個單位的速度運動, 同時,動點Q從點A出發沿著射線AB以每秒a個單位的速度運動設運動時間為t秒,
(1)求直線AB的解析式和CD的長.
(2)當△PQD與△BDC全等時,求a的值.
(3)記點P關于直線BC的對稱點為![]() ,連結
,連結![]() 當t=3,
當t=3,![]() 時, 求點Q的坐標.
時, 求點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-![]() )2 016×161 008;
)2 016×161 008;
【答案】(1)﹣10m2n3+8m3n2;(2)2x﹣40;(3)1.
【解析】試題分析:(1)原式利用單項式乘以多項式法則計算即可得到結果;
(2)原式兩項利用多項式乘以多項式法則計算,去括號合并即可得到結果;
(3)先根據冪的乘方的逆運算,把(-![]() )2 016化為(
)2 016化為(![]() )1008,再根據積的乘方的逆運算計算即可.
)1008,再根據積的乘方的逆運算計算即可.
試題解析:(1)原式=(5mn2)(﹣2mn)+(﹣4m2n)(﹣2mn)=﹣10m2n3+8m3n2;
(2)原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40.
(3)原式=(![]() )1008×161 008=(
)1008×161 008=(![]() ×16)1 008=1.
×16)1 008=1.
【題型】解答題
【結束】
19
【題目】如圖,方格圖中每個小正方形的邊長為1,點A、B、C都是格點.
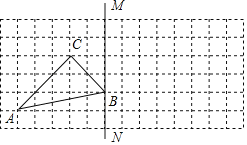
(1)畫出△ABC關于直線BM對稱的△A1B1C1;
(2)寫出AA1的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了樹立文明鄉風,推進社會主義新農村建設,某村決定組建村民文體團隊,現圍繞“你最喜歡的文體活動項目(每人僅限一項)”,在全村范圍內隨機抽取部分村民進行問卷調查,并將調查結果繪制成如下兩幅不完整的統計圖.請你根據統計圖解答下列問題:

(1)這次參與調查的村民人數為 人;
(2)請將條形統計圖補充完整;
(3)求扇形統計圖中“劃龍舟”所在扇形的圓心角的度數;
(4)若在“廣場舞、腰鼓、花鼓戲、劃龍舟”這四個項目中任選兩項組隊參加端午節慶典活動,請用列表或畫樹狀圖的方法,求恰好選中“花鼓戲、劃龍舟”這兩個項目的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
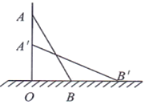
【題目】如圖,一架云梯AB長25分米,斜靠在一面墻上,梯子底端B離墻7分米.
(1)這個梯子的頂端A距地面有多高?
(2)如果梯子頂端下滑了4分米,那么梯子的底端在水平方向滑動了多少分米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E是正方形ABCD邊AB的中點,連接CE,過點B作BH⊥CE于F,交AC于G,交AD于H.下列說法: ![]() ;②點F是GB的中點;
;②點F是GB的中點; ![]() ;
; ![]() ,其中正確的結論的序號是_____________
,其中正確的結論的序號是_____________

查看答案和解析>>
科目:初中數學 來源: 題型:
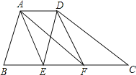
【題目】如圖,在梯形![]() 中,
中,![]() 、
、![]() 兩點分別在邊
兩點分別在邊![]() 上.
上.![]() ,
,![]() ,且四邊形
,且四邊形![]() 是平行四邊形.
是平行四邊形.
![]() 請判斷線段
請判斷線段![]() 與
與![]() 有何數量關系?并說明理由.
有何數量關系?并說明理由.
![]() 當
當![]() 時.請猜想四邊形
時.請猜想四邊形![]() 是什么特殊的平行四邊形?并說明理由.
是什么特殊的平行四邊形?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com