
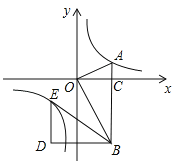
【題目】如圖,在平面直角坐標系中,OA⊥OB,AB⊥x軸于點C,點A(![]() ,1)在反比例函數
,1)在反比例函數![]() 的圖象上.
的圖象上.
(1)求反比例函數![]() 的表達式;
的表達式;
(2)在x軸的負半軸上存在一點P,使得S△AOP=![]() S△AOB,求點P的坐標;
S△AOB,求點P的坐標;
(3)若將△BOA繞點B按逆時針方向旋轉60°得到△BDE.直接寫出點E的坐標,并判斷點E是否在該反比例函數的圖象上,說明理由.
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,0);(3)E(
,0);(3)E(![]() ,﹣1),在.
,﹣1),在.
【解析】
試題分析:(1)將點A(![]() ,1)代入
,1)代入![]() ,利用待定系數法即可求出反比例函數的表達式;
,利用待定系數法即可求出反比例函數的表達式;
(2)先由射影定理求出BC=3,那么B(![]() ,﹣3),計算求出S△AOB=
,﹣3),計算求出S△AOB=![]() ×
×![]() ×4=
×4=![]() .則S△AOP=
.則S△AOP=![]() S△AOB=
S△AOB=![]() .設點P的坐標為(m,0),列出方程求解即可;
.設點P的坐標為(m,0),列出方程求解即可;
(3)先解△OAB,得出∠ABO=30°,再根據旋轉的性質求出E點坐標為(﹣![]() ,﹣1),即可求解.
,﹣1),即可求解.
試題解析:(1)∵點A(![]() ,1)在反比例函數
,1)在反比例函數![]() 的圖象上,∴k=
的圖象上,∴k=![]() ×1=
×1=![]() ,∴反比例函數的表達式為
,∴反比例函數的表達式為![]() ;
;
(2)∵A(![]() ,1),AB⊥x軸于點C,∴OC=
,1),AB⊥x軸于點C,∴OC=![]() ,AC=1,由射影定理得
,AC=1,由射影定理得![]() =ACBC,可得BC=3,B(
=ACBC,可得BC=3,B(![]() ,﹣3),S△AOB=
,﹣3),S△AOB=![]() ×
×![]() ×4=
×4=![]() ,∴S△AOP=
,∴S△AOP=![]() S△AOB=
S△AOB=![]() .
.
設點P的坐標為(m,0),∴![]() ×|m|×1=
×|m|×1=![]() ,∴|m|=
,∴|m|=![]() ,∵P是x軸的負半軸上的點,∴m=﹣
,∵P是x軸的負半軸上的點,∴m=﹣![]() ,∴點P的坐標為(
,∴點P的坐標為(![]() ,0);
,0);
(3)點E在該反比例函數的圖象上,理由如下:
∵OA⊥OB,OA=2,OB=![]() ,AB=4,∴sin∠ABO=
,AB=4,∴sin∠ABO=![]() =
=![]() =
=![]() ,∴∠ABO=30°,∵將△BOA繞點B按逆時針方向旋轉60°得到△BDE,∴△BOA≌△BDE,∠OBD=60°,∴BO=BD=
,∴∠ABO=30°,∵將△BOA繞點B按逆時針方向旋轉60°得到△BDE,∴△BOA≌△BDE,∠OBD=60°,∴BO=BD=![]() ,OA=DE=2,∠BOA=∠BDE=90°,∠ABD=30°+60°=90°,而BD﹣OC=
,OA=DE=2,∠BOA=∠BDE=90°,∠ABD=30°+60°=90°,而BD﹣OC=![]() ,BC﹣DE=1,∴E(
,BC﹣DE=1,∴E(![]() ,﹣1),∵
,﹣1),∵![]() ×(﹣1)=
×(﹣1)=![]() ,∴點E在該反比例函數的圖象上.
,∴點E在該反比例函數的圖象上.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖:在△ABC中,∠C=90°,AC=BC,過點C在△ABC外作直線MN,AM⊥MN于M,BN⊥MN于N。
(1)求證:MN=AM+BN;

(2)若過點C在△ABC內作直線MN,AM⊥MN于M,BN⊥MN于N,則AM、BN與MN之間有什么關系?請說明理由。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某運動員進行賽前訓練,如果對他30次訓練成績進行統計分析,判斷他的成績是否穩定,則需要知道這10次成績的( ).
A.眾數B.方差C.平均數D.中位數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD是平行四邊形,下列結論中不正確的是( )
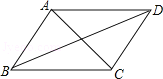
A. 當AB=BC時,它是菱形 B. 當AC⊥BD時,它是菱形
C. 當∠ABC=90°時,它是矩形 D. 當AC=BD時,它是正方形
查看答案和解析>>
科目:初中數學 來源: 題型:
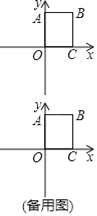
【題目】如圖,在平面直角坐標系中,四邊形OABC為矩形,點A(0,8),C(6,0).動點P從點B出發,以每秒1個單位長的速度沿射線BC方向勻速運動,設運動時間為t秒.
(1)當t= s時,以OB、OP為鄰邊的平行四邊形是菱形;
(2)當點P在OB的垂直平分線上時,求t的值;
(3)將△OBP沿直線OP翻折,使點B的對應點D恰好落在x軸上,求t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com