
【題目】(1)如圖,點![]() ,
,![]() 分別是銳角
分別是銳角![]() 兩邊上的點,
兩邊上的點,![]() ,分別以點
,分別以點![]() ,
,![]() 為圓心,以
為圓心,以![]() 的長為半徑畫弧,兩弧相交于點
的長為半徑畫弧,兩弧相交于點![]() ,連接
,連接![]() ,
,![]() .則根據作圖過程判定四邊形
.則根據作圖過程判定四邊形![]() 是菱形的依據是______.
是菱形的依據是______.
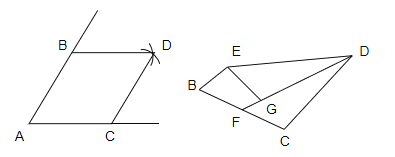
(2)如圖,在菱形![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點,將
的中點,將![]() 沿
沿![]() 翻折得到
翻折得到![]() ,射線
,射線![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,則
,則![]() ______.
______.
【答案】四條邊都相等的四邊形是菱形 ![]()
【解析】
(1)由AE=AF=ED=DF,根據四條邊都相等的四邊形是菱形,即可證得:四邊形AEDF是菱形.
(2)DE和CB的延長線相交于G'點,連結EF,作EH⊥DF于H點,如圖,根據菱形的性質得A=180°﹣∠B=120°,AB=AD=2,AD∥BC,則∠1=∠G,再利用折疊的性質得∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,則∠4=60°,在Rt△EHG中利用含30度的直角三角形三邊的關系得到HG=![]() EG=
EG=![]() ,EH=
,EH=![]() EH=
EH=![]() ,則在Rt△DEH中利用勾股定理可計算出DE=
,則在Rt△DEH中利用勾股定理可計算出DE=![]() ,再證明∠2=∠G'得到FG'=FD,證明△AED≌△BEG'得到DE=G'E,所以FE⊥DG',然后證明Rt△DEF∽Rt△DHE,利用相似比計算出DF=
,再證明∠2=∠G'得到FG'=FD,證明△AED≌△BEG'得到DE=G'E,所以FE⊥DG',然后證明Rt△DEF∽Rt△DHE,利用相似比計算出DF=![]() ,則FG=FD﹣DG=
,則FG=FD﹣DG=![]() ,于是得到BF=FG=
,于是得到BF=FG=![]() .
.
解:(1)根據作圖過程判定四邊形ABDC是菱形的依據是:四邊相等的四邊形是菱形,
理由如下:
∵根據題意得:AE=AF=ED=DF,
∴四邊形AEDF是菱形,
(2)DE和CB的延長線相交于G'點,連結EF,作EH⊥DF于H點,如圖,
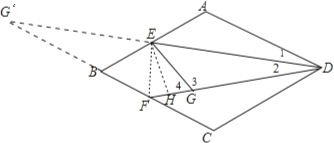
∵四邊形ABCD為菱形,
∴∠A=180°﹣∠B=120°,AB=AD=2,AD∥BC
∴∠1=∠G',
而E為AB的中點,
∴AE=BE=1,
∵△AED沿DE翻折得到△GED,
∴∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,
∴∠4=60°,
∴在Rt△EHG中,HG=![]() EG=
EG=![]() ,EH=
,EH=![]() ,
,
∵AD∥BG',
∴∠1=∠G',
∴∠G'=∠2,
∴FG'=FD,
在△AED和△BEG'中,
 ,
,
∴△AED≌△BEG',
∴DE=G'E,AD=BG'=2,
∴FE⊥DG',
∴∠FED=90°,
∵∠HDE=∠EDF,
∴Rt△DEF∽Rt△DHE,
∴![]() ,即
,即 ,
,
∴DF=![]() ,
,
∴FG=FD﹣DG=![]() ﹣2=
﹣2=![]() ,
,
∵FG'=FD,BG'=DG=2,
∴FG'-BG'=FD-DG,
∴BF=FG=![]() .
.
故答案為:(1)四條邊都相等的四邊形是菱形,(2)![]() .
.


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案科目:初中數學 來源: 題型:
【題目】兩個相似三角形,他們的周長分別是36和12.周長較大的三角形的最大邊為15,周長較小的三角形的最小邊為3,則周長較大的三角形的面積是()
A. 52 B. 54 C. 56 D. 58.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】杭州某零件廠剛接到要鑄造5000件鐵質工件的訂單,下面給出了這種工件的三視圖.已知鑄造這批工件的原料是生鐵,待工件鑄成后還要在表面涂一層防銹漆,那么完成這批工件需要原料生鐵多少噸?涂完這批工件要消耗多少千克的防銹漆?(鐵的密度為7.8g/cm3 ,1千克防銹漆可以涂4m2的鐵器面,三視圖單位為cm)
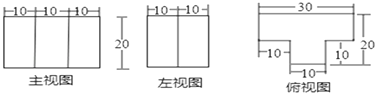
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小澤和小超分別用擲A、B兩枚骰子的方法來確定P(x,y)的位置,她們規定:小澤擲得的點數為x,小超擲得的點數為![]() ,那么,她們各擲一次所確定的點落在已知直線y=-2x+6上的概率為( )
,那么,她們各擲一次所確定的點落在已知直線y=-2x+6上的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】位于河南省鄭州市的炎黃二帝巨型塑像,是為代表中華民族之創始、之和諧、之統一.塑像由山體CD和頭像AD兩部分組成.某數學興趣小組在塑像前50米處的B處測得山體D處的仰角為45°,頭像A處的仰角為70.5°,求頭像AD的高度.(最后結果精確到0.1米,參考數據:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
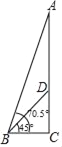
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,過點B作⊙O的切線BM,弦CD//BM,交AB于點F,且![]() ,連接AC,AD,延長AD交BM于點E.
,連接AC,AD,延長AD交BM于點E.
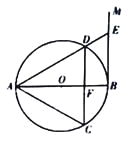
(l)求證:△ACD是等邊三角形;
(2)連接OE,若DE=2,求OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某校教學樓AB后方有一斜坡,已知斜坡CD的長為12米,坡角α為60°,根據有關部門的規定,∠α≤39°時,才能避免滑坡危險,學校為了消除安全隱患,決定對斜坡CD進行改造,在保持坡腳C不動的情況下,學校至少要把坡頂D向后水平移動多少米才能保證教學樓的安全?(結果取整數)
(參考數據:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC 中, ![]() ,D、E是斜邊BC上兩點,且∠DAE=45°,將△
,D、E是斜邊BC上兩點,且∠DAE=45°,將△![]() 繞點
繞點![]() 順時針旋轉90
順時針旋轉90![]() 后,得到△
后,得到△![]() ,連接
,連接![]() .列結論:
.列結論:
①△ADC≌△AFB;②△ ![]() ≌△
≌△![]() ;③△
;③△![]() ≌△
≌△![]() ;④
;④![]()
其中正確的是( )

A. ②④ B. ①④ C. ②③ D. ①③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com