【題目】我校草根文學社為了了解學生課外閱讀情況，抽樣調查了部分學生每周用于課外閱讀的時間，過程如下：
數據收集，從全校隨機抽取20名學生，進行了每周用于課外閱讀時間的調查，數據如下（單位：分）
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理下分段整理樣本數據并補全表格．
課外閱讀時間x（分） | 0≤x＜40 | 40≤x＜80 | 80≤x＜120 | 120≤x＜160 |
等級 | D | C | B | A |
人數 | 3 |
| 8 |
|
分析數據：補全下列表格中的統計量．
平均數 | 中位數 | 眾數 |
80 |
|
|
得出結論：
（1）用樣本中的統計量估計我校學生每周用于課外閱讀時間的情況等級為 ；
（2）假設平均閱讀一本課外書的時間為160分鐘，請你選擇樣本中的平均數估計我校學生每人一年（按52周計算）平均閱讀多少本課外書？
【答案】填表：5，4，81，81；（1）B；（2）以樣本的平均數來估計該校學生每人一年（按52周計算）平均閱讀26本課外書．
【解析】
（1）求出中位數、眾數，然后可得答案；
（2）用一周閱讀的本數乘以一年的周數即可．
填表如下：
課外閱讀時間x（分） | 0≤x＜40 | 40≤x＜80 | 80≤x＜120 | 120≤x＜160 |
等級 | D | C | B | A |
人數 | 3 | 5 | 8 | 4 |
③分析數據：補全下列表格中的統計量．
平均數 | 中位數 | 眾數 |
80 | 81 | 81 |
（1）根據上表統計顯示：樣本中位數和眾數都是81，平均數是80，都是B等級，
故估計該校學生每周的用于課外閱讀時間的情況等級為B；
（2）以平均數來估計：
×52＝26（本）．
故假設平均閱讀一本課外書的時間為160分鐘，以樣本的平均數來估計該校學生每人一年（按52周計算）平均閱讀26本課外書．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖，⊙O是△ABC的外接圓，PA是⊙O切線，PC交⊙O于點D．
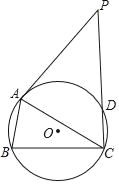
（1）求證：∠PAC＝∠ABC；
（2）若∠BAC＝2∠ACB，∠BCD＝90°，AB＝
，CD＝2，求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】天府新區某校數學活動小組在一次活動中，對一個數學問題作如下探究：
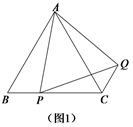
（1）問題發現：如圖1，在等邊△ABC中，點P是邊BC上任意一點，連接AP，以AP為邊作等邊△APQ，連接CQ．求證：BP CQ；
（2）變式探究：如圖2，在等腰△ABC中，ABBC，點P是邊BC上任意一點，以AP為腰作等腰△APQ，使AP PQ，APQ ABC，連接CQ．判斷∠ABC和∠ACQ的數量關系，并說明理由；
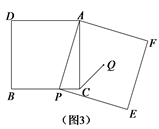
（3）解決問題：如圖3，在正方形ADBC中，點P是邊BC上一點，以AP為邊作正方形 APEF，Q是正方形APEF的中心，連接CQ．若正方形APEF的邊長為6，
，求正方形ADBC的邊長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，以AB為直徑的⊙O分別與BC，AC相交于點D，E，BD=CD，過點D作⊙O的切線交邊AC于點F.
(1)求證：DF⊥AC；
(2)若⊙O的半徑為5，∠CDF=30°，求
的長(結果保留π)．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】發現問題：
（1）如圖1，AB為⊙O的直徑，請在⊙O上求作一點P，使∠ABP＝45°．（不必寫作法）
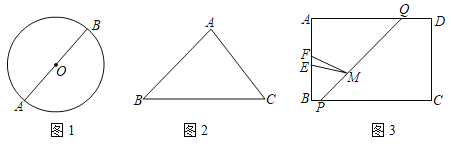
問題探究：
（2）如圖2，等腰直角三角形△ABC中，∠A＝90°，AB＝AC＝3
，D是AB上一點，AD＝2，在BC邊上是否存在點P，使∠APD＝45°？若存在，求出BP的長度，若不存在，請說明理由．
問題解決：
（3）如圖3，為矩形足球場的示意圖，其中寬AB＝66米、球門EF＝8米，且EB＝FA．點P、Q分別為BC、AD上的點，BP＝7米，∠BPQ＝135，一位左前鋒球員從點P處帶球，沿PQ方向跑動，球員在PQ上的何處才能使射門角度（∠EMF）最大？求出此時PM的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
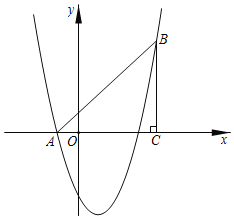
【題目】如圖，在平面直角坐標系中，已知A（﹣1，0）、C（4，0），BC⊥x軸于點C，且AC＝BC，拋物線y＝x2+bx+c經過A、B兩點．
（1）求拋物線的表達式；
（2）點E是線段AB上一動點（不與A、B重合），過點E作x軸的垂線，交拋物線于點F，當線段EF的長度最大時，求點E的坐標；
（3）在（2）的條件下，在拋物線上是否存在一點P，使△EFP是以EF為直角邊的直角三角形？若存在，求出所有點P的坐標；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
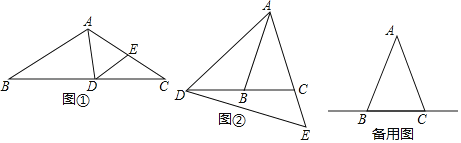
【題目】如圖，△ABC中，∠ABC=∠ACB，點D在BC所在的直線上，點E在射線AC上，且AD=AE，連接DE．
⑴如圖①，若∠B=∠C=35°，∠BAD=80°，求∠CDE的度數；
⑵如圖②，若∠ABC=∠ACB=75°，∠CDE=18°，求∠BAD的度數；
⑶當點D在直線BC上（不與點B、C重合）運動時，試探究∠BAD與∠CDE的數量關系，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】目前“微信”、“支付寶”、“共享單車”和“網購”給我們的生活帶來了很多便利，初二數學小組在校內對“你最認可的四大新生事物”進行調查，隨機調查了m人（每名學生必選一種且只能從這四種中選擇一種）并將調查結果繪制成如下不完整的統計圖．
（1）根據圖中信息求出m= ，n= ；
（2）請你幫助他們將這兩個統計圖補全；
（3）根據抽樣調查的結果，請估算全校2000名學生中，大約有多少人最認可“微信”這一新生事物？
（4）已知A、B兩位同學都最認可“微信”，C同學最認可“支付寶”D同學最認可“網購”從這四名同學中抽取兩名同學，請你通過樹狀圖或表格，求出這兩位同學最認可的新生事物不一樣的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
