
【題目】如圖所示,梯形AOCD中,AD=9,OC=10,AO=4,在線段OC上任取一點N(不與O,C重合),連接DN,作NE⊥DN,交AO于點E.

(1)當CN=2時,求點E的坐標.
(2)若CN=x,OE=y,求y與x的函數關系式.
(3)探索與研究:若點M從O點沿OC方向、N點從C點沿CO方向同時等速運動,現有一點F,滿足MF⊥MN,NF⊥ND.
①猜想F點在什么線上運動?并求出這條線所對應的函數關系式,并寫出自變量的取值范圍;
②求出F點在運動過程中的最高點的坐標.
【答案】(1)點E的坐標為(0,2);(2)①當0<x<1時,y=![]() ;②當x>1時,y=
;②當x>1時,y=![]() ;(3)①y=﹣
;(3)①y=﹣![]() x2+3x﹣
x2+3x﹣![]() (0<x<10);②最高點的坐標是(3,2).
(0<x<10);②最高點的坐標是(3,2).
【解析】試題分析:
試題解析:(1)如圖所示,作DF⊥OC于F,
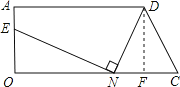
由題意知,CN=2,AD=9,OC=10.
∵AOCD是梯形且![]()
∴OF=AD=9,CF=OCOF=1,NF=CNCF=1,DF=OA=4.
∴在Rt△DFN中, ![]()
又∵NE⊥DN, ![]()
∴∠DNF=∠OEN,tan∠OEN=tan∠DNF=4.
![]()
∴點E的坐標為(0,2);
(2)如圖所示:
①當0<t<1時由(1)知CF=1,所以此時N點在F點右側,E點在y軸負半軸,
∵∠DNF=∠OEN,
![]()
整理得: ![]()
②當t>1時,如圖所示N點在F點左側,E點則在y軸正半軸,
![]()
![]()
即![]()
![]()
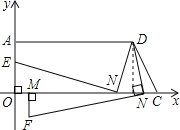
(3)①如圖所示:由圖知點F在第四象限,
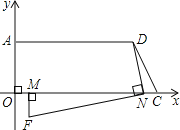
∵MF⊥MN,NF⊥ND,點F(x,y),M點、N點同時等速運動,
∴CN=
又![]()
∴∠MFN=∠DNM,
即: ![]()
y<0,
![]()
②![]()
故最高點的坐標是(3,2).


科目:初中數學 來源: 題型:
【題目】如圖,若![]() ,是
,是![]() .
.
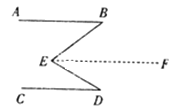
理由:如圖,過點![]() 作
作![]() ,
,
則![]() .(依據)
.(依據)
因為![]() ,
,
所以![]() ,
,
所以![]() .
.
所以![]() .
.
(1)上述證明過程中的依據是指 .
(2)若將點![]() 移至圖2所示的位置,
移至圖2所示的位置,![]() ,此時
,此時![]() 之間有什么關系?請說明理由.
之間有什么關系?請說明理由.
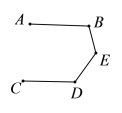
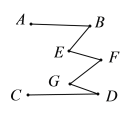
(3)在圖中,![]() ,
,![]() 與
與![]() 又有何關系?
又有何關系?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校藝術節要印制節目單,有兩個印刷廠前來聯系業務,他們的報價相同,甲廠的優惠條件是:按每份定價1.5元的八折收費,另收900元制版費;乙廠的優惠條件是:每份定價1.5元的價格不變,而900元的制版費則六折優惠.問:
(1)學校印制多少份節目單時兩個印刷廠費用是相同的?
(2)學校要印制1500份節目單,選哪個印刷廠所付費用少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在初中階段的函數學習中,我們經歷了“確定函數的表達式﹣﹣利用函數圖象研究其性質一運用函數解決問題“的學習過程.在畫函數圖象時,我們通過描點或平移的方法畫出了所學的函數圖象.同時,我們也學習了絕對值的意義|a|=![]() .
.
結合上面經歷的學習過程,現在來解決下面的問題:在函數y=|kx﹣1|+b中,當x=1時,y=3,當x=0時,y=4.
(1)求這個函數的表達式;
(2)在給出的平面直角坐標系中,請用你喜歡的方法畫出這個函數的圖象;
(3)已知函數y=![]() 的圖象如圖所示,結合你所畫的函數圖象,直接寫出不等式|kx﹣1|+b≥
的圖象如圖所示,結合你所畫的函數圖象,直接寫出不等式|kx﹣1|+b≥![]() 的解集.
的解集.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,E,F是對角線AC上的兩點,且AE=CF.下列結論:①BE=DF;②BE∥DF;③AB=DE;④四邊形EBFD為平行四邊形;⑤S△ADE=S△ABE;⑥AF=CE.其中正確的個數是( )

A. 3個 B. 4個 C. 5個 D. 6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為促進課堂教學,提高教學質量,對七年級學生進行了一次“你最喜歡的課堂教學方式”的問卷調查.根據收回的問卷,學校繪制了如下圖表,請你根據圖表中提供的信息,解答下列問題.
編號 | 教學方式 | 最喜歡的頻數 | 頻率 |
1 | 教師講,學生聽 | 20 | 0.10 |
2 | 教師提出問題,學生探索思考 | ||
3 | 學生自行閱讀教材,獨立思考 | 30 | |
4 | 分組討論,解決問題 | 0.25 |
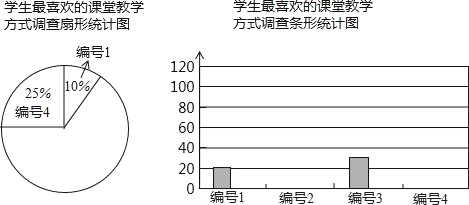
(1)收回的問卷份數為 ,把條形統計圖補充完整;
(2)扇形統計圖中編號1與編號4的圓心角分別是多少度?
(3)你最喜歡以上哪一種教學方式,請提出你的建議,并簡要說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(探究活動)
如圖1:已知直線a與b平行,直線c與直線a、b分別相交于點A. B,直線d與直線a、b分別相交于點C. D,點P在直線c上移動,連接PC、PD.探究∠CPD、∠PCA、∠PDB之間的數量關系.
(探究過程)
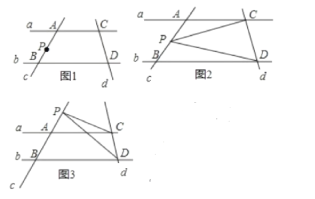
(1)當點P在點A. B之間移動時,如圖2,寫出∠CPD、∠PCA、∠PDB之間的關系,并說明理由.
(2)當點P在A. B兩點外移動時,如圖3,寫出∠CPD、∠PCA、∠PDB之間的關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 是正方形
是正方形![]() 對角線
對角線![]() 上一點,
上一點,![]() 于
于![]() ,點
,點![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點.
的中點.
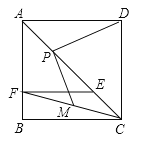
(1)求證:![]() ;
;
(2)當點![]() 在對角線
在對角線![]() (不含
(不含![]() 、
、![]() 兩點)上運動時,
兩點)上運動時,![]() 是否為定值?如果是,請求其值;如果不是,試說明理由.
是否為定值?如果是,請求其值;如果不是,試說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com