
【題目】某市舉行“行動起來,對抗霧霾”為主題的植樹活動,某街道積極響應,決定對該街道進行綠化改造,共購進甲、乙兩種樹共50棵,已知甲樹每棵800元,乙樹每棵1200元.
(1)若購買兩種樹的總金額為56000元,求甲、乙兩種樹各購買了多少棵?
(2)若購買甲樹的金額不少于購買乙樹的金額,至少應購買甲樹多少棵?
 小學課時特訓系列答案
小學課時特訓系列答案科目:初中數學 來源: 題型:
【題目】以下說法合理的是:( )
A. “打開電視,正在播放新聞節日”是必然事件
B. “拋一枚硬幣,正面朝上的概率為![]() ”表示每拋兩次就有一次正面朝上
”表示每拋兩次就有一次正面朝上
C. “拋擲一枚均勻的骰子,出現點數6的概率是![]() ”表示隨著拋擲次數的增加“出現點數6”這一事件發生的頻率穩定在
”表示隨著拋擲次數的增加“出現點數6”這一事件發生的頻率穩定在![]() 附近
附近
D. 為了解某品牌火腿的質量,選擇全面檢測
查看答案和解析>>
科目:初中數學 來源: 題型:
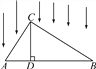
【題目】如圖所示,△ABC被平行光線照射,CD⊥AB于D,AB在投影面上.
(1)指出圖中AC的投影是什么?CD與BC的投影呢?
(2)探究:當△ABC為直角三角形(∠ACB=90°)時,易得AC2=AD·AB,此時有如下結論:直角三角形一直角邊的平方等于它在斜邊射影與斜邊的乘積,這一結論我們稱為射影定理.通過上述結論的推理,請證明以下兩個結論.
①BC2=BD·AB;②CD2=AD·BD.
查看答案和解析>>
科目:初中數學 來源: 題型:
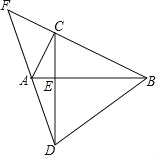
【題目】如圖,Rt△ABC中,∠ACB=90°,CD⊥AB于E,CD=AB,DA、BC延長線交于F.
(1)若AC=12,∠ABC=30°,求DE的長;
(2)若BC=2AC,求證:DA=![]() FC.
FC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P為邊長為2的正方形ABCD的對角線BD上任一點,過點P作PE⊥BC于點E,PF⊥CD于點F,連接EF.給出以下4個結論:①AP=EF;②AP⊥EF;③EF最短長度為![]() ;④若∠BAP=30°時,則EF的長度為2.其中結論正確的有( )
;④若∠BAP=30°時,則EF的長度為2.其中結論正確的有( )
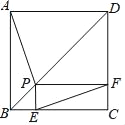
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,三角形![]() (記作
(記作![]() )在方格中,方格紙中的每個小方格都是邊長為1個單位的正方形,三個頂點的坐標分別是
)在方格中,方格紙中的每個小方格都是邊長為1個單位的正方形,三個頂點的坐標分別是![]() ,
,![]() ,
,![]() ,先將
,先將![]() 向上平移3個單位長度,再向右平移2個單位長度,得到
向上平移3個單位長度,再向右平移2個單位長度,得到![]() .
.

(1)在圖中畫出![]() ;
;
(2)點![]() ,
,![]() 的坐標分別為______、______;
的坐標分別為______、______;
(3)若![]() 軸有一點
軸有一點![]() ,使
,使![]() 與
與![]() 面積相等,求出
面積相等,求出![]() 點的坐標.
點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電子廠生產一種新型電子產品,每件制造成本為20元,試銷過程中發現,每月銷售量y(萬件)與銷售單價x(元)之間的關系可以近似地看作一次函數y=﹣2x+100.(利潤=售價﹣制造成本)
(1)寫出每月的利潤z(萬元)與銷售單價x(元)之間的函數關系式;
(2)當銷售單價為多少元時,廠商每月獲得的利潤為400萬元?
(3)根據相關部門規定,這種電子產品的銷售單價不能高于40元,如果廠商每月的制造成本不超過520萬元,那么當銷售單價為多少元時,廠商每月獲得的利潤最大?最大利潤為多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
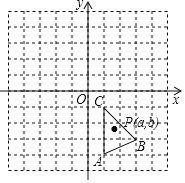
【題目】如圖,在平面直角坐標系中,△ABC的三個頂點坐標分別為A(1,-4),B(3,-3),C(1,-1).
(1)將△ABC先向上平移5個單位,再向左平移3個單位,畫出平移后得到的△A1B1C1;
(2)寫出△A1B1C1各頂點的坐標;
(3)若△ABC內有一點P(a,b),請寫出平移后得到的對應點P1的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
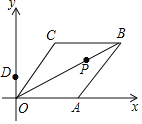
【題目】已知菱形OABC在平面直角坐標系的位置如圖所示,頂點A(5,0),OB=4![]() ,點P是對角線OB上的一個動點,D(0,1),當CP+DP最短時,點P的坐標為( )
,點P是對角線OB上的一個動點,D(0,1),當CP+DP最短時,點P的坐標為( )
A. (0,0)B. (1,![]() )C. (
)C. (![]() ,
,![]() )D. (
)D. (![]() ,
,![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com