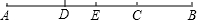【答案】
分析:(1)先根據BE平分∠ABC,CE平分∠BCD可知∠ABC=2∠1,∠BCD=2∠2,再根據四邊形ABCD是平行四邊形可知∠ABC+∠BCD=180°,即2(∠1+∠2)=∠ABC+∠BCD=180°,進而可得出結論;
(2)由BE平分∠ABC,可知∠1=∠3,再根據四邊形ABCD可知AD∥BC,∠1=∠5,∠3=∠5,故可得出AB=AE,同理可證,DC=DE,再由平行四邊形的性質即可得出結論;
(3)由(1)(2)可知,在圖2中,∠BEC=90°,AB=AG,CD=DF,設AB=CD=x,依題意,BC=AD=3x,AG=DF=x,故可得出GF=3x-2x=x,
作EN⊥BC,交BC于N,交AD于M,則ME=EN-MN,由AD∥BC可得出△EBC∽△EFG,根據相似三角形的性質即可得出結論.
解答:解:(1)在圖1,圖2,圖3中,
∵BE平分∠ABC,CE平分∠BCD,
∴∠ABC=2∠1,∠BCD=2∠2,
∵?ABCD,
∴∠ABC+∠BCD=180°,
∴2(∠1+∠2)=∠ABC+∠BCD=180°,
∴∠1+∠2=90°,
∴∠BEC=90°;

(2)圖2中,∵BE平分∠ABC,
∴∠1=∠3,
∵?ABCD,
∴AD∥BC,
∴∠1=∠5,
∴∠3=∠5,
∴AB=AE,
同理可證,DC=DE,
∵四邊形ABCD是平行四邊形,
∴AB=DC,BC=AD,
∴BC=2AB,
∴

=2;
(3)在圖3中,
由(1)(2)可知,在圖2中,∠BEC=90°,AB=AG,CD=DF,
設AB=CD=x,依題意,BC=AD=3x,AG=DF=x,
∴GF=3x-2x=x,
作EN⊥BC,交BC于N,交AD于M,
則ME=EN-MN,
∵AD∥BC,
∴△EBC∽△EFG,
∴

,
∴

=3,
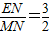
,
∴

=

×

=

.
[方法II]由(1)(2)可知,在圖4中,∠BEC=90°,AB=AG,CD=DF,
設AB=CD=x,依題意,BC=AD=3x,AG=DF=x,
∴GF=3x-2x=x,
作GI∥AB交BC于I,作FJ∥AB交BC于J,
易證菱形ABIG,菱形GIJF,菱形FJCD,
且這三個菱形等底等高,
因而三個菱形的面積相等.

設三個菱形的面積均為S,則S
2=3S,
∵BG為菱形ABIG的對角線,CF為菱形DCJF的對角線,
∴S
△BIG=S
△CEJ=

S
∴S
梯形FGBC=2S,
∴S
梯形FGBC=

S
2,
∵AD∥BC,
∴△EBC∽△EFG,
∴

,
∴

,
∴
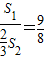
,
∴

.
點評:本題考查的是相似形綜合題,涉及到相似三角形的判定與性質、平行四邊形的性質、平行線的性質等相關知識,涉及面較廣,難度較大.


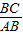 的值;
的值;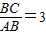 時(圖3),求
時(圖3),求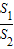 的值.
的值.
 =2;
=2; ,
, =3,
=3,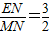 ,
, =
= ×
× =
= .
.
 S
S S2,
S2, ,
, ,
,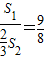 ,
, .
.

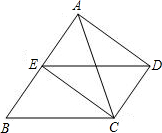 已知,如圖,DC∥AB,且DC=
已知,如圖,DC∥AB,且DC=