
【題目】如圖,等邊△ABD與等邊△ACE,連接BE、CD,BE的延長線與CD交于點F,下列結論:(1)BE=CD ;(2)AF平分∠EAC ; (3)∠BFD=60°;(4)AF+FD=BF 其中正確的有( )
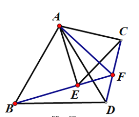
A.1個B.2個C.3個D.4個
【答案】C
【解析】
(1)先證△BAE≌△DAC,即可得到BE=CD;
(2)利用四點共圓的判定證出A、E、F、C四點共圓,再利用反證法假設(2)成立得到與條件矛盾即可說明假設不成立;
(3)根據A、E、F、C四點共圓,可求出∠EFC,然后就可求∠BFD;
(4)利用截長補短法:在BF上找到點G使得FG=FA,先證△AFG是等邊三角形,再證
△BAG≌△DAF即可證出結論.
在BF上找到點G使得FG=FA,如下圖所示:
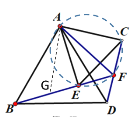
∵△ABD和△ACE是等邊三角形
∴∠BAD=∠EAC=60°,AB=AD,AE=AC
∴∠BAD-∠EAD=∠EAC-∠EAD
∴∠BAE=∠DAC,
在△BAE和△DAC中,

∴△BAE≌△DAC,(SAS)
∴BE=CD,故(1)正確;
∠BEA=∠ACD,
∵∠AEB+∠AEF=180°,
∴∠AEF+∠ACF=180°,
∴A、E、F、C四點共圓,
∴假設(2)正確,即∠EAF=∠CAF
由圓的性質可得EF=FC
∴∠FEC=∠FCE
∴∠FEC+∠AEC=∠FCE+∠ACE
∴∠AEF=∠ACF
又∵∠AEF+∠ACF=180°(已證)
∴∠AEF=∠ACF=90°
而題中的∠AEF是動角,不一定是90°,矛盾,
故(2)不一定正確;
∵A、E、F、C四點共圓,∠EAC=60°
∴∠EFC=120°,
∴∠BFD=180°-∠EFC =60°,故(3)正確;
∵AE=AC,
∴∠AFC=∠AFE=![]() ∠EFC=60°
∠EFC=60°
∵FG=FA,
∴△AFG是等邊三角形,
∴AG=AF,∠FAG=60°
∵∠BAG+∠GAD=60°,∠FAD+∠GAD =60°,
∴∠BAG =∠FAD,
在△BAG和△DAF中,
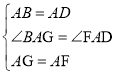
∴△BAG≌△DAF(SAS),
∴BG=FD,
∴AF+FD=FG+BG=BF,故(4)正確;
∴正確的結論有3個.
故選C.


科目:初中數學 來源: 題型:
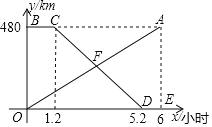
【題目】甲、乙兩地相距480km,一輛貨車從甲地勻速駛往乙地,貨車出發一段時間后,一輛汽車從乙地勻速駛往甲地,設貨車行駛的時間為![]() 線段OA表示貨車離甲地的距離
線段OA表示貨車離甲地的距離![]() 與xh的函數圖象;折線BCDE表示汽車距離甲地的距離
與xh的函數圖象;折線BCDE表示汽車距離甲地的距離![]() 與
與![]() 的函數圖象.
的函數圖象.
![]() 求線段OA與線段CD所表示的函數表達式;
求線段OA與線段CD所表示的函數表達式;
![]() 若OA與CD相交于點F,求點F的坐標,并解釋點F的實際意義;
若OA與CD相交于點F,求點F的坐標,并解釋點F的實際意義;
![]() 當x為何值時,兩車相距100千米?
當x為何值時,兩車相距100千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在△ABC中,CD、CE分別是△ABC的高和角平分線,∠BAC=α,∠B=β(α>β).

(1)若α=70°,β=40°,求∠DCE的度數;
(2)試用α、β的代數式表示∠DCE的度數(直接寫出結果);
(3)如圖②,若CE是△ABC外角∠ACF的平分線,交BA延長線于點E,且α﹣β=30°,求∠DCE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,甲、乙只捕撈船同時從A港出海捕魚,甲船以每小時15![]() km的速度沿北偏西60°方向前進,乙船以每小時15 km的速度沿東北方向前進.甲船航行2 h到達C處,此時甲船發現漁具丟在了乙船上,于是甲船快速(勻速)沿北偏東75°的方向追趕乙船,結果兩船在B處相遇.問:
km的速度沿北偏西60°方向前進,乙船以每小時15 km的速度沿東北方向前進.甲船航行2 h到達C處,此時甲船發現漁具丟在了乙船上,于是甲船快速(勻速)沿北偏東75°的方向追趕乙船,結果兩船在B處相遇.問:
(1)甲船從C處出發追趕上乙船用了多少時間?
(2)甲船追趕乙船的速度是每小時多少千米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是過點
是過點![]() 的一條直線,且點
的一條直線,且點![]() 在線段
在線段![]() 上時,
上時,![]() 于點
于點![]() ,
,![]() 于點
于點![]() .易證:
.易證:![]() .
.

(1)如圖②,點![]() 在線段
在線段![]() 的延長線時,其余條件不變,問
的延長線時,其余條件不變,問![]() 與
與![]() ,
,![]() 的關系如何?請證明;
的關系如何?請證明;
(2)如圖③,點![]() 在線段
在線段![]() 的延長線時,其余條件不變,問
的延長線時,其余條件不變,問![]() 與
與![]() 的關系如何?請直接寫出結果,不需證明.
的關系如何?請直接寫出結果,不需證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的面積為1cm2,對角線交于點O;以AB、AO為鄰邊作平行四邊形AOC1B,對角線交于點O1;以AB、AO1為鄰邊作平行四邊形AO1C2B…;依此類推,則平行四邊形AO2016C2017B的面積為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖, △ABC中,AB=AC,D在AC上,E在BC上,A E,B D交于F,∠AFD=60°,∠FDC+∠FEC=180°.

(1)求證:BE=CD.
(2)如圖2,過點D作DG⊥AF于G,直接寫出AE ,FG, BF的關系.
(3)如圖3,在(2)的條件下,連接CG,若FG=BF,△AGD的面積等于5,求GC的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,六邊形ABCDEF∽六邊形GHIJKL,相似比為2:1,則下列結論正確的是( )

A. ∠E=2∠K B. BC=2HI C. 六邊形ABCDEF的周長=六邊形GHIJKL的周長 D. S六邊形ABCDEF=2S六邊形GHIJKL
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=30°,點M,N分別在邊OA,OB上,OM=5,ON=12,點P,Q分別在邊OB,OA上運動,連接MP,PQ,QN,則MP+PQ+QN的最小值為 ______ .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com